微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
www.^91exam.org
江 苏
一、填空题
1.已知集合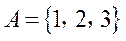 ,
,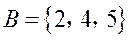 ,则集合
,则集合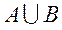 中元素的个数为_______.
中元素的个数为_______.
2.已知一组数据4,6,5,8,7,6,那么这组数据的平均数为________.
3.设复数z满足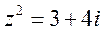 (i是虚数单位),则z的模为_______.
(i是虚数单位),则z的模为_______.
4.根据如图所示的伪代码,可知输出的结果S为________.

5.袋中有形状、大小都相同的4只球,其中1只白球,1只红球,2只黄球,从中一次随机摸出2只球,则这2只球颜色不同的概率为________.
6.已知向量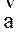 =(2,1),
=(2,1),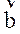 =(1,-2),若
=(1,-2),若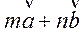 =(9,-8)(m,n
=(9,-8)(m,n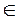 R),则m-n的值为______.
R),则m-n的值为______.
7.不等式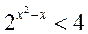 的解集为________.
的解集为________.
8.已知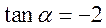 ,
,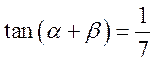 ,则
,则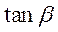 的值为_______.
的值为_______.
9.现有橡皮泥制作的底面半径为5,高为4的圆锥和底面半径为2、高为8的圆柱各一个。若将它们重新制作成总体积与高均保持不变,但底面半径相同的新的圆锥和圆柱各一个,则新的底面半径为 。
10.在平面直角坐标系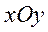 中,以点
中,以点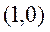 为圆心且与直线
为圆心且与直线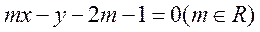 相切的所有圆中,半径最大的圆的标准方程为 。
相切的所有圆中,半径最大的圆的标准方程为 。
11.数列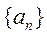 满足
满足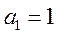 ,且
,且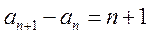 (
(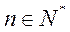 ),则数列
),则数列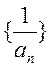 前10项的和为 。
前10项的和为 。
12.在平面直角坐标系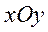 中,
中,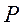 为双曲线
为双曲线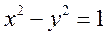 右支上的一个动点。若点
右支上的一个动点。若点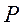 到直线
到直线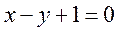 的距离大于c恒成立,则是实数c的最大值为 。
的距离大于c恒成立,则是实数c的最大值为 。
13.已知函数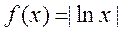 ,
,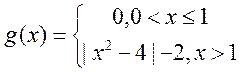 ,则方程
,则方程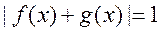 实根的个数为 。
实根的个数为 。
14.设向量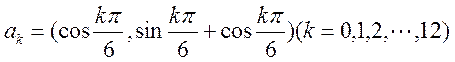 ,则
,则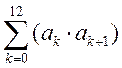 的值为 。
的值为 。
15.在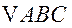 中,已知
中,已知
(1)求BC的长;
(2)求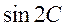 的值。
的值。
16.如图,在直三棱柱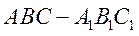 中,已知
中,已知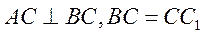 .设
.设 的中点为D,
的中点为D,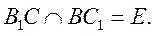
求证:(1)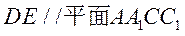
(2)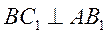

17.(本小题满分14分)某山区外围有两条相互垂直的直线型公路,为进一步改善山区的交通现状,计划修建一条连接两条公路和山区边界的直线型公路,记两条相互垂直的公路为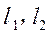 ,山区边界曲线为C,计划修建的公路为l,如图所示,M,N为C的两个端点,测得点M到
,山区边界曲线为C,计划修建的公路为l,如图所示,M,N为C的两个端点,测得点M到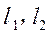 的距离分别为5千米和40千米,点N到
的距离分别为5千米和40千米,点N到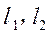 的距离分别为20千米和2.5千米,以
的距离分别为20千米和2.5千米,以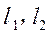 所在的直线分别为x,y轴,建立平面直角坐标系xOy,假设曲线C符合函数
所在的直线分别为x,y轴,建立平面直角坐标系xOy,假设曲线C符合函数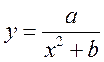 (其中a,b为常数)模型.
(其中a,b为常数)模型.
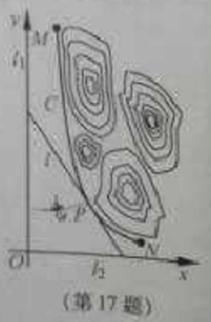
(I)求a,b的值;
(II)设公路l与曲线C相切于P点,P的横坐标为t.
①请写出公路l长度的函数解析式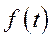 ,并写出其定义域;
,并写出其定义域;
②当t为何值时,公路l的长度最短?求出最短长度.
18.(本小题满分16分)
如图,在平面直角坐标系xOy中,已知椭圆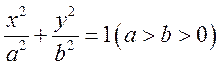 的离心率为
的离心率为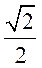 ,且右焦点F到左准线l的距离为3.
,且右焦点F到左准线l的距离为3.
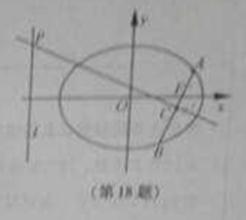
(1)求椭圆的标准方程;
(2)过F的直线与椭圆交于A,B两点,线段AB的垂直平分线分别交直线l和AB于点P,C,若PC=2AB,求直线AB的方程.
19.
已知函数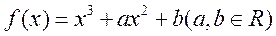 。
。
(1)试讨论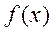 的单调性;
的单调性;
(2)若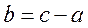 (实数c是与a无关的常数),当函数
(实数c是与a无关的常数),当函数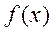 有三个不同的零点时,a的取值范围恰好是
有三个不同的零点时,a的取值范围恰好是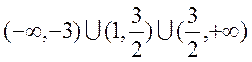 ,求c的值。
,求c的值。
20.设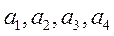 是各项为正数且公差为d
是各项为正数且公差为d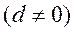 的等差数列
的等差数列
(1)证明: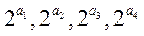 依次构成等比数列;
依次构成等比数列;
(2)是否存在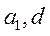 ,使得
,使得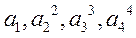 依次构成等比数列?并说明理由;
依次构成等比数列?并说明理由;
(3)是否存在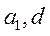 及正整数
及正整数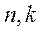 ,使得
,使得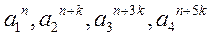 依次构成等比数列?并说明理由。
依次构成等比数列?并说明理由。
附加题
21、(选做题)本题包括A、B、C、D四小题,请选定其中两小题,并在相应的区域内作答,若多做,则按作答的前两小题评分,解答时应写出文字说明、证明过程或演算步骤。
A、 选修4-1:几何证明选讲
选修4-1:几何证明选讲 (本小题满分10分)
(本小题满分10分)
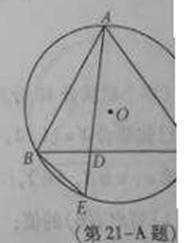
如图,在 中,
中,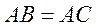 ,
, 的外接圆
的外接圆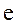 O的弦
O的弦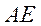 交
交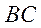 于点D
于点D
求证: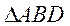
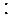
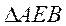

B、 选修4-2:矩阵与变换
选修4-2:矩阵与变换 (本小题满分10分)
(本小题满分10分)
已知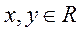 ,向量
,向量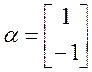 是矩阵
是矩阵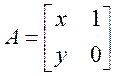 的属于特征值
的属于特征值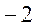 的一个特征向量,矩阵
的一个特征向量,矩阵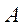 以及它的另一个特征值。
以及它的另一个特征值。
C.[选修4-4:坐标系与参数方程]
已知圆C的极坐标方程为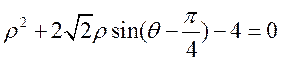 ,求圆C的半径.
,求圆C的半径.
D.[选修4-5:不等式选讲]
解不等式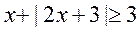
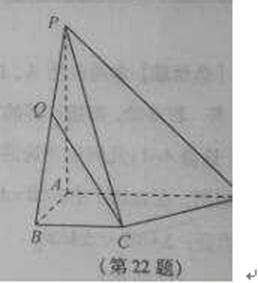
22.如图,在四棱锥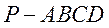 中,已知
中,已知 平面
平面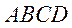 ,且四边形
,且四边形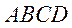 为直角梯形,
为直角梯形,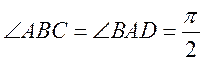 ,
,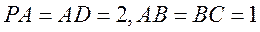
(1)求平面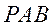 与平面
与平面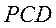 所成二面角的余弦值;
所成二面角的余弦值;
(2)点Q是线段BP上的动点,当直线CQ与DP所成角最小时,求线段BQ的长
23.已知集合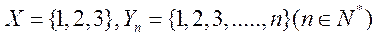 ,设
,设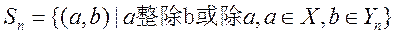 ,令
,令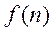 表示集合
表示集合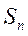 所含元素的个数.
所含元素的个数.
(1)写出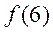 的值;
的值;
(2)当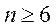 时,写出
时,写出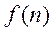 的表达式,并用数学归纳法证明。
的表达式,并用数学归纳法证明。






