1、实验题  用游标卡尺和螺旋测微器分别测量某一工件的长度和内径如下图所示，则被测工件长度为________cm ，内径为?mm 。

参考答案：5.45? 8.476-8.479

本题解析：游标卡尺读数方法：首先读出游标尺0刻线对应的主尺的整数部分读作n毫米，然后读出游标尺第几个刻度线和主尺刻度线对齐，读作m，最后读数为：(m+n×0.1)mm，所以本题读作54.5mm或5.45cm.
螺旋测微器的读数包括两部分：大于0．5mm的刻度值由主尺读出，用m表示；小于0．5mm的刻度值由旋轮(即可动刻度)读出，用n表示，可动刻度要估读一位，则螺旋测微器所测量的值为m+0.01n，单位为毫米。所以本题读作8.476～8.479mm
点评：容易题。虽然游标卡尺度数反复要求，但是总有学生掌握不住，希望学生掌握这种方法，不要死记硬背。

本题难度：简单

2、计算题  （16分）如图所示，原长分别为L1和L2、劲度系数分别为k1和k2的轻质弹簧竖直悬挂在天花板上。两弹簧之间有一质量为m1的物体，最下端挂着质量为m2的另一物体，整个装置处于静止状态。
（1）这时两个弹簧的总长度为多大？
（2）若用一个质量为M的平板把下面的物体竖直缓慢地向上托起，直到两个弹簧的总长度等于两弹簧的原长之和，求这时平板受到下面物体m2的压力。

参考答案：（1）L1+L2++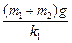
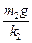
（2）FN＇=+m2g

本题解析：（1）劲度系数为k1轻质弹簧受到的向下拉力（m1+m2）g，设它的伸长量为x1，根据胡克定律有：（m1+m2）g=k1 x1?（2分）
解得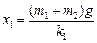：?（2分）
劲度系数为k2轻质弹簧受到的向下拉力m2g，设它的伸长量为x2，根据胡克定律有：
m2g=k2 x2?（2分）
解得：?（2分）
这时两个弹簧的总长度为：L=L1+L2+x1+x2=L1+L2+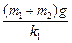+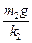?（2分）
（2）根据题意，下面的弹簧应被压缩x，上面的弹簧被拉伸x。
以m1为对象，根据平衡关系有??（k1+k2）x=m1g?（2分）
解得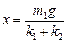：?（1分）
以m2为对象，设平板对m2的支持力为FN，根据平衡关系有?
FN=k2x+m2g=+m2g?（2分）
故这时平板受到下面物体m2的压力?FN＇=+m2g?（1分）

本题难度：一般

3、实验题  在“验证机械能守恒定律”实验中，

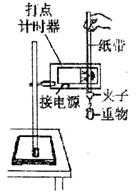
I. 第一组同学用打点计时器按照图示装置进行实验，则
（1）对于自由下落的重物，下述选择的条件哪种更为有利?（?）
A. 只要足够重就可以。
B. 只要体积足够小就可以。
C. 既要足够重，又要体积非常小。
D. 因为不需要知道动能和势能的具体数值，不需要测量重物的质量，所以对重物可任意选择。
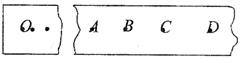
（2）已知打点计时器所用电源的频率为50Hz。查得当地的重力加速度g=9.80m／s2，测得所用的重物的质量为1.00kg。实验中得到一条点迹清晰的纸带，如图所示，把第一个点记作O，在纸带上另取连续4个点A、B、C、D作为测量的点，经测量知道A、B、C、D各点到O点的距离分别为62.99cm、70.18cm、77.76cm、85.73cm。根据以上数据，可知重物由O点运动到C点，重力势能减少量等于?J，动能的增加量等于?J。（取3位有效数字）

II. 第二组同学利用下图所示的实验装置，验证钩码和滑块所组成的系统从由静止释放到通过光电门这一过程机械能守恒。实验开始时，气轨已经调成水平状态。

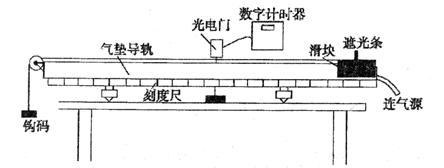
（1）已知遮光条的宽度为d，实验时将滑块从图示位置由静止释放，由数字计时器读出遮光条通过光电门的时间为t，则滑块经过光电门时的速度为?。
（2）在本次实验中还需要测量的物理量有（文字说明并用相应的字母表示）：钩码的质量m、?和?。
3）本实验通过比较?和?（用测量的物理量符号表示）在实验误差允许的范围内是否相等，从而验证系统的机械能是否守恒。

参考答案：Ⅰ. （1）C?（2）7.62? 7.56
Ⅱ. （1）d/t?（2）滑块的质量M?释放时挡光片到光电门的距离L
（3）? mgL

本题解析：Ⅰ. （1）小球的质量越大，体积越小所受空气阻力越小，C对；（2）重力势能减小量mgh,C点速度可根据BD平均速度去求Ⅱ. （1）滑块经过光电门时可看作匀速，速度为d/t （2）根据机械能守恒关系式可知需要测量的物理量为滑块的质量M?释放时挡光片到光电门的距离L（3）略

本题难度：简单

4、选择题  如图所示，质量分别为m1和m2的两物块放在水平地面上，与水平地面间的动摩擦因数都是μ（μ≠0），用轻质弹簧将两物块连接在一起，当用水平力F作用在m2上时，两物体均以加速度a做匀加速运动，此时，弹簧伸长量为x；?当用水平力F′作用在m2上时，两物体均以加速度2a做匀加速运动，此时，弹簧伸长量为x′，则下列关系正确的是（　　）
A．F′=2F
B．x′=2x
C．F′＞2F
D．x′＜2x