1、实验题  某同学设计了一个用打点计时器验证动量守恒的实验，在小车A的前端和小车B的后端贴有粘扣，在木板的右端固定打点计时器，小车A后面拖一长纸带，木板下垫有小木块，用来平衡摩擦力，反复移动小木块的位置，直到小车在木板上运动时可保持匀速直线运动状态，现使小车A，B分别静止在木板的右端和中间，如图所示，给小车A一个瞬时冲量，小车A与静止的小车B相碰并粘合成一体，并继续做匀速直线运动，已知打点计时器电源频率为50 Hz。若得到打点纸带如图所示，并得各计数点之间的距离，A点为运动的起点，则应选段___________计算小车A碰撞前的速度，应选段__________计算两车碰撞后的速度，若测得小车A的质量m1=0.4 kg，小车B的质量m2=0.2 kg，由以上数据可得，小车A，B碰撞前的总动量为___________kg·m/s；碰撞后的总动量为___________kg·m/s；得到的结论是___________________________。（保留小数点后三位）

参考答案：BC，DE，0.420，0.417，在误差允许的范围之内碰撞动量守恒

本题解析：

本题难度：一般

2、简答题  在绝缘水平面上放置一质量为m=2.0×10-3kg的带电滑块A，电量为q=1.0×10-7C.在A的左边L=1.2m处放置一个不带电的滑块B，质量为M=6.0×10-3kg，滑块B距左边竖直绝缘墙壁s=0.6m，如图所示.在水平面上方空间加一方向水平向左的匀强电场，电场强度为E=4.0×105N/C，A由静止开始向左滑动并与B发生碰撞，设碰撞的过程极短，碰撞后两滑块结合在一起共同运动并与墙壁相碰撞，在与墙壁发生碰撞时没有机械能损失，两滑块始终没有分开，两滑块的体积大小可以忽略不计.已知A、B与地面的动摩擦因数均为μ=0.5。试通过计算，在坐标图中作出滑块A从开始运动到最后静止的速度——时间图象．（取g=10m/s2）

参考答案：请看解析

本题解析：设A和B相遇时的速度为v1，相碰后共同运动的速度为v.
根据动能定理，对滑块A有：（qE—μmg）L =" m" v12/2?………2分
解得:v1="6m/s?" …………1分
滑块A从开始运动到与B相碰所用的时间为：
?……………2分
代入数据解得：? 2分
A、B碰撞动量守恒，有：mv1=（M+m）v?…………2分
得：?………1分
滑块A与B碰撞后结合在一起，电场力大小仍然为：
F=qE=1.0×10-7C×4.0×105N/C=4.0×10-2N.方向向左 …………1分
两滑块的摩擦力为： f=μ（m+M）g? ……1分
代入数据解得：f = 4.0×10-2N，方向向右
所以，A、B碰撞后一起以速度v向着墙壁作匀速直线运动.A、B碰后到运动到墙壁处所用的时间为：
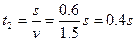?………1分
A、B一起与墙壁碰撞后，两滑块受到的电场力与摩擦力大小不变，方向都向左，所以A、B与墙壁碰撞后一起以速度v向右做减速运动，直至速度减为零，最后静止.所经历的时间设为t3

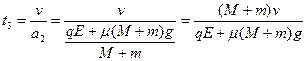
代入数据解得：?………2分
v——t图象如图，（每对一段给1分）

本题难度：简单

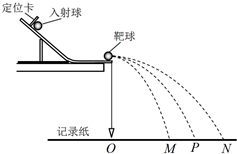
3、填空题  如图所示为“验证动量守恒定律”的实验装置．

（1）下列说法中符合本实验要求的是______．（选填选项前面的字母）
A．入射球比靶球质量大或者小均可，但二者的直径必须相同
B．在同一组实验的不同碰撞中，每次入射球必须从同一高度由静止释放
C．安装轨道时，轨道末端必须水平
D．需要使用的测量仪器有天平、刻度尺和秒表
（2）实验中记录了轨道末端在记录纸上的竖直投影为O点，经多次释放入射球，在记录纸上找到了两球平均落点位置为M、P、N，并测得它们到O点的距离分别为OM、OP和ON．已知入射球的质量为m1，靶球的质量为m2，如果测得m1?

参考答案：（1）A、在小球碰撞过程中水平方向动量守恒定律故有m1v0=m1v1+m2v2
在碰撞过程中动能守恒故有12m1v02=12m1v12+12m2v22
解得v1=m1-m2m1+m2v0?
要碰后入射小球的速度v1＞0，即m1-m2＞0，即入射球要比靶球质量大，
要发生水平方向的对心碰撞，故二者的直径必须相同
故答案A错误．
B、在同一组的实验中要保证入射球和靶球每次平抛的速度都相同，故每次入射球必须从同一高度由静止释放．故B正确．
C、要保证每次小球都做平抛运动，则轨道的末端必须水平．故C正确．
D、本实验不需要测小球平抛运动的速度，故不需要测运动的时间，所以不需要秒表．故D错误．
故选BC．
（2）在小球碰撞过程中水平方向动量守恒定律故有m1v0=m1v1+m2v2
即有m1v0t=m1v1t+m2v2t
故有m1.OP=m1.OM+m2.ON
故答案为m1.OP?
若在碰撞过程中动能守恒则有12m1v02=12m1v12+12m2v22
即12m1?.OP2=12m1.OM2+12m2.ON2
又由于m1.OP=m1.OM+m2.ON
联立以上两式可得.OM+.OP=.ON
故答案为.ON
故本题的答案为：（1）BC
（2）m1.OP，.ON．

本题解析：

本题难度：一般

4、简答题  在固定的光滑水平杆(杆足够长)上，套有一个质量为m＝0.5 kg的光滑金属圆环。一根长为L＝1 m的轻绳，一端拴在环上，另一端系着一个质量为M＝2 kg的木块，如图所示。现有一质量为m0＝20 g的子弹以v0＝1 000 m/s的水平速度射穿木块，子弹穿出木块后的速度为v＝200 m/s(不计空气阻力和子弹与木块作用的时间)，求：
(1)当子弹射穿木块后，木块向右摆动的最大高度为多大?
(2)当木块第一次返回到最低点时，木块的速度是多大?
(3)当木块第一次返回到最低点时，水平杆对环的作用力是多大?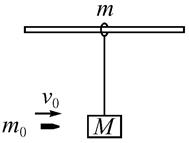

参考答案：(1)8 m/s? (2)4.8 m/s? (3)153 N

本题解析：(1)设子弹从木块中穿出时木块的速度为v1，在子弹与木块相互作用的过程中两者动量守恒
m0v0＝m0v＋Mv1
解得v1＝8 m/s
在木块与圆环一起向右运动的过程中，两者满足水平方向动量守恒Mv1＝(M＋m)v2
机械能守恒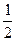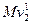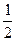＝?(M＋m)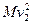＋Mgh
解得 h＝0.64 m
(2)木块从最高点返回最低点的过程中，由水平方向动量守恒得 (M＋m)v2＝mv3＋Mv4
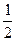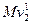机械能守恒(M＋m)＋Mgh＝＋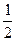
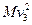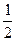
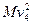
解得 v3＝12.8 m/s v4＝4.8 m/s
v3＝0 v4＝8 m/s(舍去)
(3)第一次返回到最低点时，木块的速度v4＝4.8 m/s，圆环的速度v3＝12.8 m/s绳子拉力T1－Mg＝M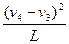
解得T1＝148 N
水平杆对环的作用力N1＝T1＋mg＝153 N。

本题难度：简单

5、计算题  在光滑水平面上有三个小滑块，A、B用细线相连，中间有一压缩的弹簧（弹簧与滑块不拴接），在滑块B上的中间部位放有一个可视为质点的小滑块C。已知弹簧最初的弹性势能Ep=1.35J，A、B、C三个滑块的质量分别为mＡ＝3kg，mB＝2kg，mC＝1kg，B与C间的动摩擦因数为μ=0.2，B的右端距固定在地面上的竖直弹性挡板P的距离为L=0.5m。现剪断AB间的细绳，A、B弹开（A、B从弹开到与弹簧分离的时间极短，忽略不计），一段时间后B与P发生弹性正碰，整个运动过程中C一直没有滑离B的表面。（g取10m/s2）

（1）A、B弹开后，通过相应计算判断B碰到挡板P前是否与C达到共同速度。
（2）求出A、B、C三个物体的最终速度大小。
（3）B滑块长度的最小值。

参考答案：1）B碰前已经与C达共同速度
（2）vＡ＝0.6m/s? vB＝vC＝0.2m/s
（3）B最小长度为0.27m

本题解析：略

本题难度：简单