1、计算题  (19分)如图，在xoy平面上x<0的区域内存在一垂直纸面向外的匀强磁场，磁感应强度大小为B；OA是过原点的一条直线，与y轴正方向夹角为60°．在x>0的区域有一与OA平行的匀强电场，场强大小为E．现有一质量为m，电量为q的带正电的粒子(重力不计)从直线OA上的某处P点由静止释放后，经0点进入磁场，经过一段时间后恰能垂直OA到达0A上的Q点(电场方向以及P点、Q点位置在图中均未画出)．求

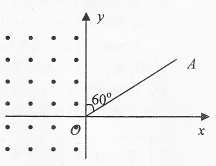
(1)P点的坐标；
(2)粒子从P点释放到垂直0A到达Q点所用的时间；
(3)PQ之间的距离．

参考答案：解：（1）设P点坐标为(x，y)，粒子到达O点时速度为v1，
粒子在电场中加速度a=qE/m，①
v12=2a·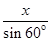，②?
粒子从O点进入后做匀速圆周运动，设运动半径为R，则有，
qv1B=m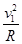，③

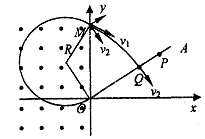
粒子从M点射出磁场再次进入电场，速度大小为v1，方向与y轴负方向成60°角，设到达Q点时速度为v2，则：v2=v1sin60°，④
又由几何关系可知，OM之间的距离为d="2R" sin60°，⑤
设粒子从M点到Q点所用时间为t3，则，dsin60°= v2t3，⑥
v1cos60°="a" t3，⑦
联立解得：x=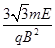，⑧
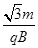t3=。⑨
由几何关系可得：y==。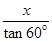
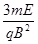即P点坐标为：(,).。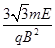
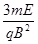（2）设粒子从P点到O点所用的时间为t1，从O点到M点所用的时间为t2，则，
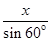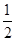=at12，
解得t1=。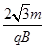
粒子从O点进入磁场后做匀速圆周运动的周期为：T=，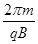
t2=2T/3=。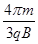
所以从P点释放到垂直OA经过Q点所用时间为t= t1+ t2+t3=。
（3）由①④⑦⑨得：v2=3E/B..。
设PQ之间的距离为l，在整个运动过程中，由动能定理，qEl=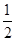mv22，
解得：l=。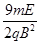

本题解析：分析带电粒子在电场磁场中的运动情况，应用带电粒子在电场、磁场中运动的相关知识列方程解答。

本题难度：一般

2、计算题  （15分）如图所示，直线OA与x轴成135°角，x轴上下方分别有水平向右的匀强电场E1和竖直向上的匀强电场E2，且电场强度E1＝E2＝10N/C，x轴下方还存在垂直于纸面向外的匀强磁场B，磁感应强度B＝10T。现有一质量m＝1.0×10－5kg，电荷量q＝1.0×10－5C的带正电尘粒在OA直线上的A点静止释放，A点离原点O的距离d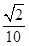＝m(g取10m/s2，)．求：

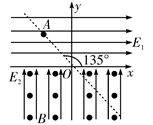
(1)尘粒刚进入磁场区域时的速度v的大小；
(2)从进入磁场区域开始到离开磁场区域所经历的时间t；
(3)第一次回到OA直线上的某位置离原点O的距离L。

参考答案：（1）2m/s（2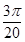）s（3）0.13m

本题解析：(1)F=Eq=1×10－4N?， 1分?
尘粒在电场E中受到的合外力为
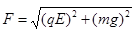?，1分?
合外力F和水平方向间的夹角φ为tanφ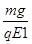＝＝1
φ＝45°?
尘粒在电场E1中的加速度a大小为a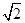＝g ， 2分
v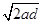＝＝2m/s?，2分?
(2)进入磁场后尘粒在磁场中转动的周期T和转动半径R分别为
T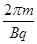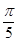＝＝s，2分
R＝＝0.2m? 2分
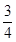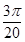轨迹如图所示，由图可知，t＝T＝s? 2分
(3)出磁场后尘粒在电场E1中做类平抛运动
OC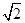＝R＝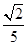
t1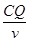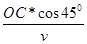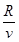＝＝＝＝0.1s? 2分
B位置离原点O的距离L大小为
L＝OC·sin45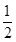－at1＝R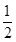－at1＝0.13m? 2 分
点评：电荷在匀强磁场中做匀速圆周运动，关键是画出轨迹，由几何知识求出半径．定圆心角，求时间．

本题难度：一般

3、选择题  如图所示，在真空中，匀强电场E的方向竖直向下，水平匀强磁场B垂直纸面向里，三个液滴a、b、c带有等量同种电荷。已知a静止，油滴b水平向右匀速运动，油滴c水平向左匀速运动。三者质量ma、mb和mc相比较 （?）

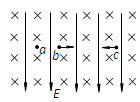
A．ma>mb>mc
B．mb>ma>mc
C．mc>ma>mb
D．ma=mb=mc

参考答案：C

本题解析：共点力作用下物体平衡专题．
分析：三个带电油滴都受力平衡，根据共点力平衡条件列式求解即可．
解：a球受力平衡，有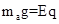?①
重力和电场力等值、反向、共线，故电场力向上，由于电场强度向下，故球带负电；
b球受力平衡，有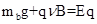?②
c球受力平衡，有?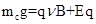?③
解得mc>ma>mb

本题难度：简单

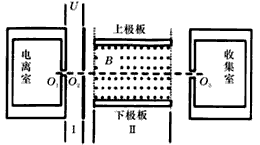
4、计算题  有人设想用下图所示的装置来选择密度相同、大小不同的球状纳米粒子。粒子在电离室中电离后带正电，电量与其表面积成正比。电离后，粒子缓慢通过小孔O1进入极板间电压为U的水平加速电场区域I，再通过小孔O2射入相互正交的恒定匀强电场、磁场区域II，其中磁场的磁感应强度大小为B，方向如图。收集室的小孔O3与O1、O2在同一条水平线上。半径为r0的粒子，其质量为m0、电量为q0，刚好能沿O1O3直线射入收集室。不计纳米粒子重力。（）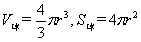
（1）试求图中区域II的电场强度；
（2）试求半径为r的粒子通过O2时的速率；
（3）讨论半径r≠r0的粒子刚进入区域II时向哪个极板偏转。

参考答案：解：（1）设半径为r0的粒子加速后的速度为v0，则


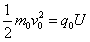
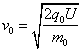
设区域II内电场强度为E，则
v0q0B=q0E
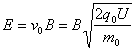，电场强度方向竖直向上
（2）设半径为r的粒子的质量为m、带电量为q、被加速后的速度为v，则


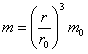
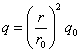
由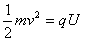，得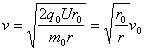
（3）半径为r的粒子，在刚进入区域II时受到合力为：F合=qE-qvB=qB(v0-v)
由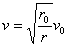可知，当
r>r0时，v＜v0，F合>0，粒子会向上极板偏转
r＜r0时，v>v0，F合＜0，粒子会向下极板偏转

本题解析：

本题难度：困难

5、计算题  如图所示，在垂直于光滑水平地面的竖直线A1A2的右侧的广阔区域，分布着竖直向上的匀强电场和平行于地面指向读者的匀强磁场。在地面上停放着一辆质量为M的绝缘小车，车的左、右两端竖直固定着一对等大的平行带电极板（构成电容为C的平行板电容器，板距为L），分别带电荷量为+Q和—Q，其中右极板紧靠A1A2线，下端开有一小孔。现有一带正电的小物块（电荷量为q、质量为m），从A1A2线上距右板下端小孔高为H处，以速度 v0水平向右射入电、磁场区域，恰在竖直平面内做圆周运动，且正好从右板下端的小孔切入小车底板的上表面，并立即贴着上表面滑行，但不会与左板相碰。已知小物块与车板面间的动摩擦因数为μ，两极板和小物块的电荷量始终保持不变，当地重力加速度为g。求：
小题1:A1A2线右侧电场的场强E和磁场的磁感应强度B的大小；
小题2:小物块在小车内运动离小车右板的最大距离。

参考答案：
小题1: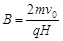
小题2: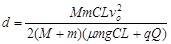

本题解析：（1）由小物块在竖直平面内做圆周运动可知：
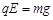? ①（1分）
解得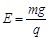：?（1分）
物块在竖直平面内做圆周运动的半径：
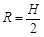? ②（1分）
根据牛顿第二定律及洛伦兹力公式：
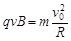? ③（1分）
由以上两式解得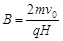：?（1分）
（2）设两极板间匀强电场的场强为E0，两板间电压为U，则：
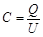?? ④（1分）
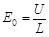? ⑤（1分）
设物块进入小车的加速度大小为a1，方向向右，根据牛顿第二定律：
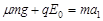? ⑥（1分）
设小车的加速度大小为a2，方向向左，根据牛顿第二定律：
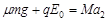? ⑦（1分）
设物块和小车达共同速度所需时间为t，根据运动学公式：
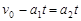? ⑧（1分）
设物块滑至距右板的最大距离为d，则：
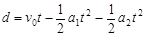?⑨（1分）
联立以上各式解得：
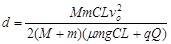? ⑩（1分）

本题难度：一般