1、计算题  （16分）如图所示，宽度为L=1m的某一区域存在相互垂直的匀强电场E和匀强磁场B，其大小E=2×108N/C，B=1T。一带正电的粒子以基本一初速度由M点垂直电场和磁场进入，沿直线从N点离开；若只撤去磁场，则粒子从P与水平成450角射出。

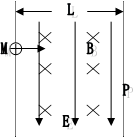
（1）求粒子的比荷
（2）若只撤去电场，则粒子以与水平方向成多少度角穿出

参考答案：（1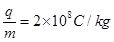）?（2）θ=370

本题解析：（1）沿直线运动，Bqv="Eq" (2分) 解得v=2×108m/s (1分)
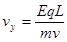类平抛运动：（1分）?（2分）
(2分)?联立解得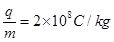?(2分)
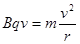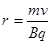（2）圆周运动半径r：?（2分）?（1分）
代入数据解得r=1m?（1分）
设穿出时角度为θ：? (1分)
得θ=370?（1分）
点评：学生明确只有电场时，粒子做类平抛运动，只有磁场时，粒子做匀速圆周运动，要作出粒子运动的轨迹，找出圆心和半径。

本题难度：一般

2、计算题  如图所示，Oxyz为空间直角坐标系，其中Oy轴正方向竖直向上。在整个空间中存在竖直向下的匀强磁场，磁感应强度大小为B。现有一质量为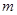、电荷量为q（q＞0）的带电小球从坐标原点O以速度v0沿Ox轴正方向射出，重力加速度为g，空气阻力可忽略不计。

（1）若在整个空间加一匀强电场，小球从坐标原点O射出恰好做匀速圆周运动，求所加电场的场强大小，以及小球做匀速圆周运动第一次通过z轴的z坐标；
（2）若改变第（1）问中所加电场的大小和方向，小球从坐标原点O射出恰好沿Ox轴做匀速直线运动，求此时所加匀强电场的场强大小；
（3）若保持第（2）问所加的匀强电场不变而撤去原有的磁场，小球从坐标原点O以速度v0沿Ox轴正方向射出后，将通过A点，已知A点的x轴坐标数值为xA，求小球经过A点时电场力做功的功率。

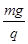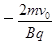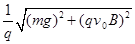参考答案：（1），（2）（3）

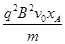
本题解析：（1）设所加电场场强大小为E1，由于带电小球从坐标原点O射出在电场和磁场共存的区域做匀速圆周运动，所以带电小球受到的电场力必定与重力平衡，有 qE1=mg。
解得?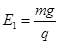
设带电小球做匀速圆周运动的半径为R，
根据牛顿第二定律和向心力公式?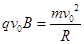，解得?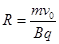
带电小球第一次通过z轴的z坐标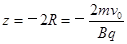
（2）设所加电场场强大小为E2，带电小球做匀速直线运动，它所受重力mg、洛伦兹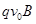力以及电场力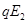三力合力为零。
因洛伦兹力沿z轴的负方向，重力沿y轴的负方向，
所以电场力?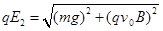
解得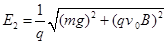
（3）当撤去磁场后，带电小球只受电场力和重力作用，这两个力的合力大小为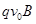，方向指向Oz正方向，所以小球在xOz平面做匀变速曲线运动。
带电小球沿Ox轴正方向以v0做匀速直线运动，小球从坐标原点O射出，运动到A点所用时间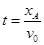
带电小球沿Oz轴正方向做初速为零的匀加速直线运动，其加速度大小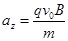
带电小球到A点时沿Oz正方向的分速度大小为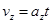
因重力在这个过程中不做功，小球经过A点时，电场力做功的功率等于合外力在此时的瞬时功率，解得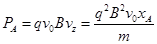
点评：本题个解题关键是根据小球的运动情况分析所加电场的大小和方向，圆周运动就是让电场力平衡重力，匀速直线运动就是让电场力、重力、洛伦兹力合力为零，在第（3）问中要注意小球受到的合力大小等于洛伦兹力大小，方向与之相反，小球做类平抛运动。

本题难度：一般

3、选择题  如图所示，L1和L2为平行线，L1上方和L2下方都是垂直纸面向里的磁感应强度相同的匀强磁场，AB两点都在L2上．带电粒子从A点以初速v与L2成30°斜向上射出，经过偏转后正好过B点，经过B点时速度方向也斜向上，不计重力，下列说法中正确的是：

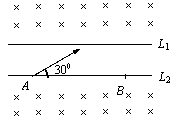
A．带电粒子经过B点时的速度一定跟在A点的速度相同。
B．若带电粒子在A点时的初速度变大（方向不变），该粒子仍能经过B点。
C．若只将带电粒子的电量增大，其它不变，该粒子一定不能经过B点。
D．带电粒子一定带正电荷。

参考答案：AB

本题解析：洛仑兹力不做功，所以A,B两点速度大小相同，又因为题目中说B点时速度方向也斜向上；A对；
根据运动的对称性，速度变大粒子运动的弦长变大，速度方向也不变，所以仍能通过B点；
与电性无关，所以选AB。

本题难度：简单

4、计算题  如图所示为一种测量电子比荷的仪器的原理图，其中阴极K释放电子，阳极A是一个中心开孔的圆形金属板，在KA间加一定的电压。在阳极右侧有一对平行正对带电金属板M、N，板间存在方向竖直向上的匀强电场。O点为荧光屏的正中央位置，且K与O的连线与M、N板间的中心线重合。电子从阴极逸出通过KA间的电场加速后从小孔射出，沿KO连线方向射入M、N两极板间。已知电子从阴极逸出时的初速度、所受的重力及电子之间的相互作用均可忽略不计，在下列过程中，电子均可打到荧光屏上。
（1）为使电子在M、N两极板间不发生偏转，需在M、N两极板间加一个垂直纸面的匀强磁场，请说明所加磁场的方向；
（2）如果M、N极板间的电场强度为E，垂直纸面的匀强磁场的磁感应强度为B，K与A间的电压为U，电子恰能沿直线KO穿过M、N两极板，打在荧光屏正中央，求电子的比荷（电荷量和质量之比）为多少；
（3）已知M、N板的长度为L1，两极板右端到荧光屏的距离为L2，如果保持M、N两极板间的电场强度为E，K与A间的电压为U，而撤去所加的磁场，求电子打到荧光屏上的位置与O点的距离。

参考答案：解：（1）电子在电场和磁场重叠的空间不发生偏转，必是电场力与洛仑兹力大小相等，方向相反，而电场力方向竖直向下，洛伦兹力方向一定竖直向上，由左手定则可判定磁场方向垂直纸面向外
（2）电子穿过电场和磁场区域沿直线运动，必受力平衡，0? ①
电子经电压为U的电场加速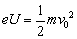 ②
联立①②解得电子的比荷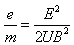
（3）电子通过M、N两极板间的过程中，在竖直方向做初速为零的匀加速运动，在水平方向做匀速直线运动
电子在两极板间运动时间t1=，加速度
所以电子在两极板间竖直方向的位移=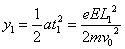
电子离开两极板间后做匀速直线运动，运动时间t2=
电子从极板右端射出时其沿竖直方向的速度=
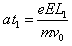
电子离开两极板间后，竖直方向的位移=
电子打到荧光屏上的位置与O点的距离

本题解析：

本题难度：困难

5、选择题  场强为E的匀强电场和磁感强度为B的匀强磁场正交．如图质量为m的带电粒子在垂直于磁场方向的竖直平面内，做半径为R的匀速圆周运动，设重力加速度为g，则下列结论不正确的是（　　）
A．粒子带负电，且q=