1、填空题  （1）图（a）所示螺旋测微器的读数为______?mm；图（b）所示游标卡尺的读数为______?cm．

（2）如图C示，某同学用插针法测定一半圆形玻璃砖的折射率．在平铺的白纸上垂直纸面插大头针P1、P2确定入射光线，并让入射光线过圆心O，在玻璃砖（图中实线部分）另一侧垂直纸面插大头针P3，使P3挡住P1、P2的像，连接OP3．图中MN为分界面，虚线半圆与玻璃砖对称，B、C分别是入射光线、折射光线与圆的交点，AB、CD均垂直于法线并分别交法线于A、D点．
①设AB的长度为L1，AO的长度为L2，CD的长度为L3，DO的长度为L4，为较方便地表示出玻璃砖的折射率，需用刻度尺测量______，则玻璃砖的折射率可表示为______．
②该同学在插大头针P3前不小心将玻璃砖以O为圆心顺时针转过一小角度，由此测得玻璃砖的折射率将______?（填“偏大”、“偏小”或“不变”）．

参考答案：（1）螺旋测微器的固定刻度读数为3.5mm，可动刻度读数为0.01×20.0mm=0.200mm，所以最终读数为3.700mm．
游标卡尺的固定刻度读数为6mm，游标读数为0.1×2mm=0.2mm，所以最终读数为6mm+0.2mm=6.2mm=0.62cm．
故本题答案为：3.700，0.62；
（2）①根据几何知识得，入射角的正弦sini=ABBO，折射角的正弦sinr=CDOC=l3OC，又BO=OC，则折射率为n=sinisinγ=l1l3．故需要测量的量有l1 和l3；
②该同学在插大头针P3前不小心将玻璃砖以O为圆心顺时针转过一小角度，折射光线将顺时针转动，而作图时仍以MN为边界，AD为法线，则入射角不变，折射角减小，由折射率公式律n=sinisinγ可知，测得玻璃砖的折射率将偏大．
故答案为：①l1 和l3；n=l1l3；②偏大．

本题解析：

本题难度：简单

2、计算题  水平传送带以v=2m/s速度匀速运动，将物体轻放在传送带的A端，它运动到传送带另一端B所需时间为11s，物体和传送带间的动摩擦因数μ=0.1，求：
小题1:传送带AB两端间的距离？
小题2:若想使物体以最短时间到达B端，则传送带的速度大小至少调为多少？（g=10m/s2）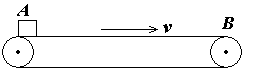

参考答案：
小题1:20m
小题2:2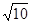m/s

本题解析：（1）物体运动的加速度为：a=μg= 1m/s2
加速运动的时间为：t=Vt/a=2/1=2s
因为物块从A到B只用了1秒。
所以AB间的距离为：s=1/2at2+Vt(11-t) =20m
(2)要使想使物体以最短时间到达B端，则要使物体一直做加速运动
当物体一直做加速运动时有
Vt2-Vo2=2as
Vt2=2x1x20
解得：Vt=2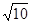m/s
所以，传送带的速度大小至少调为2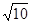m/s

本题难度：简单

3、简答题  在2001年发生在美国的“9.11”事件中，有一名职员为求生存，从110层跳了下来．已知每层楼的高度为4米，如果认为此人在整个过程中做的是自由落体运动．（g=10m/s2）求此人：
（1）整个下落过程中所用的时间是多少？
（2）此人落在地面上时的瞬时速度为多大？

参考答案：（1）由S=12gt2有t=

本题解析：

本题难度：一般

4、选择题  如图所示，一水平传送带以不变的速度v向右运动，将质量为m的物体A轻轻放在传送带左端，经时间t后，A的速度也变为v，再经过时间t后，恰好到达右端。则(? )

A．A由传送带左端到右端的平均速度为3v/4
B．传送带的长度为2vt
C．A与传送带之间的动摩擦因数为2v/gt
D．摩擦力对A先做正功后做负功

参考答案：A

本题解析：加速过程的平均速度为0.5v,所以加速运动的位移为0.5vt,水平传送带的长度为0.5vt+vt=1.5vt,平均速度为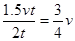，A对；B错；由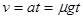可知动摩擦因数为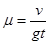，C错；物体在传送带上相对静止后不受摩擦力的做用，所以摩擦力先做正功后不做功，D错；
点评：物体在传送带上匀速运动所受摩擦力为零，这是判断摩擦力做功正负的关键，其他问题根据牛顿第二定律和运动学公式不难求解，本题难度较易

本题难度：一般

5、选择题  对于做初速度为零的匀加速直线运动的物体，以下叙述中正确的是
A.相邻的相等时间间隔内的位移之差为常数
B.相邻的相等时间间隔内的位移之差为最初的那个相等时间间隔内位移差的两倍
C.该物体运动过程中任意两个相等的时间间隔内的速度改变量均相等
D.该物体运动过程中任意两个相等的时间间隔内位移大小之比一定是奇数

参考答案：AC

本题解析：分析：对初速度为零的匀变速直线运动规律的综合运用应掌握好三个基本公式：
v=at

v2=2ax
解答：
A、令初速度为v0，相等时间为T，加速度为a，则第1个T内的位移为：

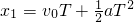
第2个T时间内的初速度为v1=v0+aT
则第2个T内的位移为

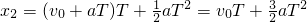
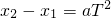∴为一常量，故A正确；
B、由A分析知∴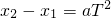为一常量，为开始时Ts内位移的2倍，故B正确；
C、据v=at得：△v=a△t，即时间相等则速度改变量相等，故C正确；
D、据得，从开始起连续相等时间内的位移比为连续奇数比，而选项任意两个时间间隔内的位移比则不一定为奇数，故D错误．
故选AC．
点评：注意对初速度为零的匀加速直线运动规律的认知，注意规律的成立条件，不能死记结论，不知成立条件．

本题难度：困难