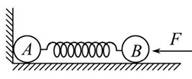
1、选择题  如图所示，质量均为m的A、B两球之间系着一根不计质量的弹簧，放在光滑的水平面上，A球紧靠竖直墙壁.今用水平力F将B球向左推压弹簧，平衡后，突然将F撤去，在这一瞬间

①B球的速度为零，加速度为零?
②B球的速度为零，加速度大小为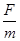
③在弹簧第一次恢复原长之后，A才离开墙壁
④在A离开墙壁后，A、B两球均向右做匀速运动
以上说法正确的是(? )
A.只有①? B.②③? C.①④? D.②③④

参考答案：B.

本题解析：撤去F前，B球受四个力作用，竖直方向的重力和支持力平衡，水平方向推力F和弹簧的弹力平衡，即弹簧的弹力大小为F，撤去F的瞬间，弹簧的弹力仍为F，故B球所受合外力为F，则B球加速度为a=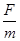?，而此时B球的速度为零，②正确①错误；在弹簧恢复原长前，弹簧对A球有水平向左的弹力使A球压紧墙壁，直到弹簧恢复原长时A球才离开墙壁，A球离开墙壁后，由于弹簧的作用，使A、B两球均做变速运动，③对④错，B选项正确.

本题难度：一般

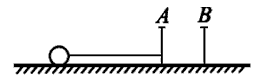
2、计算题  如图所示，光滑的水平面上钉有两枚铁钉A和B，相距0.1 m．长1m的柔软细绳拴在A上，另一端系一质量为0.5 kg的小球．小球的初始位置在AB连线上A 的一侧，把细线拉紧，给小球以2 m/s的垂直细线方向的水平速度使它做圆周运动．由于钉子B的存在，使细线慢慢地缠在A、 B上．
(1)如果细线不会拉断，那么从小球开始运动到细线完全缠在A、B上需要多长时间？
(2)如果细线的抗断拉力为7N，那么从小球开始运动到细线拉断需经历多少时间？

参考答案：解：
在小球做匀速圆周运动的过程中，由于细绳不断缠在A、B上，其轨道半径逐渐减小．小球受到的绳子的拉力提供向心力，即，且F随R的减小而增大，而运动的半周期随绳长的减小而减小．推算出每个半周期的时间及周期数，就可求出总时间．根据绳子能承受的最大拉力，可求出细绳拉断所经历的时间．
在第一个半周期内：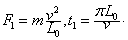
在第二个半周期内：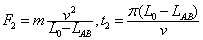
在第三个半周期内：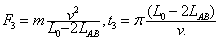
在第n个半周期内：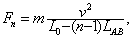
由于，所以n≤10．
(1)小球从开始运动到细线完全缠到A、B上的时间 t=t1+t2+…+t10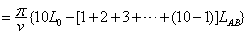

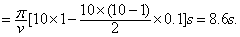
(2)设在第x个半周期时，Fx=7 N．由Fx= ，代入数据后解得x=8，则所经历的时间：

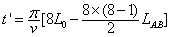
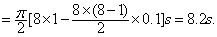
本题解析：

本题难度：困难

3、选择题  甲、乙两物体都做匀速圆周运动，其质量之比为1：2，运动轨道半径之比为1：2．当甲转过60°时，乙转过了45°，则它们所受的合外力大小之比为（　　）
A．1：4
B．2：3
C．3：16
D．4：9

参考答案：当甲转过60°时，乙转过了45°，根据ω=△θ△t知，角速度之比为4：3．
根据F合=mrω2得，甲乙的质量比为1：2，轨道半径比为1：2．角速度之比为4：3．知所受的合外力之比为4：9．故D正确，A、B、C错误．
故选D．

本题解析：

本题难度：简单

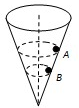
4、选择题  如图所示，一个内壁光滑的圆锥筒的轴线是竖直的，圆锥固定，有质量相同的两个小球A和B贴着筒的内壁在水平面内做匀速圆周运动，A球的运动半径较大，则（　　）
A．A球的角速度小于B球的角速度
B．A球的线速度小于B球的线速度
C．A球运动的向心加速度大小等于B球的向心加速度
D．A球对筒壁的压力大于B球对筒壁的压力