1、简答题  如图所示，质量为60kg的滑雪运动员，在倾角θ为30°的斜坡顶端，从静止开始匀加速下滑90m到达坡底，用时10s．若g取10m/s2，求
（1）运动员下滑过程中的加速度大小；
（2）运动员到达坡底时的速度大小；
（3）运动员受到的合外力大小．

参考答案：（1）根据位移时间公式，有
x=12at2
解得
a=2xt2=2×90100=1.8m/s2
即运动员下滑过程中的加速度大小为1.8m/s2．
（2）根据速度时间公式
v=at=1.8×10=18m/s
即运动员到达坡底时的速度大小为18m/s．
（3）根据牛顿第二定律，有
F=ma=60×1.8=108N
即运动员受到的合外力大小为108N．

本题解析：

本题难度：一般

2、计算题  在一次抗洪救灾工作中，一架直升机A用长H＝50 m的悬索(重力可忽略不计)系住一质量m＝50 kg的被困人员B，直升机A和被困人员B以v0＝10 m/s的速度一起沿水平方向匀速运动，如图甲所示．某时刻开始收悬索将人吊起，在5 s时间内，A、B之间的竖直距离以l＝50－t2(单位：m)的规律变化，取g＝10 m/s2。
(1)求这段时间内悬索对被困人员B 的拉力大小
(2)直升机在t＝5 s时停止收悬索，但发现仍然未脱离洪水围困区，为将被困人员B尽快运送到安全处，飞机在空中旋转后静止在空中寻找最近的安全目标，致使被困人员B在空中做圆周运动，如图乙所示．此时悬索与竖直方向成37°角，不计空气阻力，求被困人员B做圆周运动的线速度以及悬索对被困人员B的拉力．(sin 37°＝0.6，cos 37°＝0.8)

参考答案：解：（1）被困人员在水平方向上做匀速直线运动，在竖直方向上被困人员的位移y＝H－l＝50－(50－t2)＝t2，由此可知，被困人员在竖直方向上做初速度为零、加速度a＝2 m/s2的匀加速直线运动
由牛顿第二定律可得F－mg＝ma
解得悬索的拉力F＝m(g＋a)＝600 N
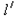（2）=H－y＝25 m，旋转半径r＝sin 37°
由＝mgtan 37°
解得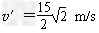
此时被困人员B的受力情况如图所示

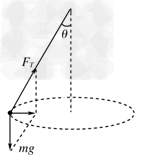
由图可知FTcos 37°＝mg，解得FT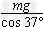＝＝625 N

本题解析：

本题难度：一般

3、计算题  通过测试得知某型号的卡车在某种路面上急刹车时加速度的大小是5m/s2 。如果要求它在这种路面上行驶时在22.5m内必须停下，它的行驶速度不能超过多少千米每小时？

参考答案：54km/h

本题解析：略

本题难度：简单

4、计算题  一物体由斜面底端上滑到顶端恰好静止，历时，那么它从斜面中点到顶端所用的时间是多少？

参考答案：解：反过来后它是一个初速度为零的匀加速直线运动，这时可以用简单的比例关系求解，如图.
C→A过程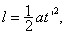①
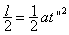C→B过程②
②/①解得t”=1 s．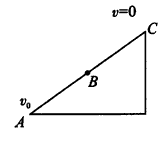

本题解析：

本题难度：一般

5、简答题  （6分）矿井里的升降机从静止开始做匀加速直线运动，上升3s，速度达到3m/s,然后匀速上升6s，最后减速上升2s停下，升降机上升的高度为________，在方框中画出升降机运动的v一t图像。

参考答案：25.5（m）

本题解析：矿井里的升降机运动的速度－时间图象如图所示

如图示，v—t图像求高度，图像所围成的面积数值上等于位移的大小
S＝S梯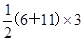＝＝25.5（m）

本题难度：简单