1、计算题  如图所示，一束电子（电量为e）以速度v0垂直射入磁感应强度为B，宽为d的匀强磁场中，穿出磁场时速度方向与电子原来入射方向的夹角为30°，则电子的质量是多少？穿过磁场的时间是多少？
　　　

参考答案：解析：电子在磁场中运动，只受洛伦兹力作用，故其轨迹是圆弧一部分，又因为f⊥v，故圆心在电子穿入和穿出磁场时受到洛伦兹力指向的交点上，如图16－60中的O点．由几何知识可知：AB间的圆心角θ＝30°，OB为半径．
r＝d/sin30°＝2d，又由r＝mv/Be得m＝2dBe/v．
由于AB圆心角是30°，故穿透时间t＝T/12＝πd/3v．
点拨：带电粒子的匀速圆周运动的求解关键是画出匀速圆周运动的轨迹，利用几何知识找出圆心及相应的半径，从而找到圆弧所对应的圆心角

本题解析：略

本题难度：一般

2、选择题  两个粒子，带电荷量相等，在同一匀强磁场中只受磁场力而做匀速圆周运动．则下列说法正确的是(　　)
A．若速率相等，则半径必相等
B．若质量相等，则周期必相等
C．若质量相等，则半径必相等
D．若动能相等，则周期必相等

参考答案：B

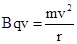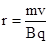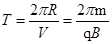本题解析：两个粒子，带电荷量相等，在同一匀强磁场中只受磁场力而做匀速圆周运动，有得：，．利用这两个公式进行判断。
A、粒子在磁场中洛伦兹力提供向心力，做匀速圆周运动．则有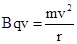得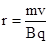：，由于带电粒子们的m不相同，所以r不同，A项错误，
B、由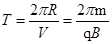，可知若质量相等，则周期必相等，B正确；
C、粒子在磁场中洛伦兹力提供向心力，做匀速圆周运动．则有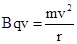得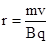：，由于带电粒子的v不相同，所以r不同，C项错误，．
D、由周期公式得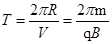：，若动能相等，质量不一定相同，所以周期不一定相同．故D错误。
故选：B．
点评：带电粒子在磁场、质量及电量相同情况下，运动的半径与速率成正比，从而根据运动圆弧来确定速率的大小；运动的周期均相同的情况下，可根据圆弧的对应圆心角来确定运动的时间的长短．

本题难度：简单

3、选择题  质子和α粒子由静止开始，经同一电场加速后，沿垂直于磁场的方向射入同一匀强磁场中，则质子和α粒子在磁场中运动的各量之间的关系，正确的是（?）
A．速率之比为∶1
B．周期之比为1∶2
C．半径之比为∶1
D．向心力之比为2∶1

参考答案：AB

本题解析：α粒子的电荷量是质子的2倍，质量是质子的4倍.
设加速电压为U，加速后的速度为v，根据动能定理有：
qU=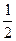mv2，v=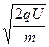，质子和α粒子的速率之比
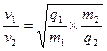=∶1，A对.根据r=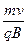公式得半径之比
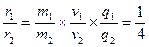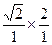×=∶2，C错.周期之比
,B对.向心力就是洛伦兹力F=qBv,
=∶2,D错.

本题难度：简单

4、计算题  科学家推测，宇宙中可能有由反粒子组成的反物质存在，反粒子与正粒子有相同的质量，却带有等量的异号电荷..1998年6月，我国科学家研制的阿尔法磁谱仪由美国“发现号”航天飞机搭载升空，寻找宇宙中反物质存在的证据.磁谱仪的核心部分如图所示，PQ、MN是两个平行板，它们之间存在匀强磁场区，磁场方向与两板平行.宇宙射线中的各种粒子从板PQ中央的小孔O垂直PQ进入匀强磁场区，在磁场中发生偏转，并打在附有感光底片的板MN上，留下痕迹.假设宇宙射线中存在氢核、反氢核、氦核、反氦核四种粒子，它们以相同速度v从小孔O垂直PQ板进入磁谱仪的磁场区，并打在感光底片上的a、b、c、d四点，已知氢核质量为m，电荷量为e，PQ与MN间的距离为L，磁场的磁感应强度为B.
（1）指出a、b、c、d四点分别是由哪种粒子留下的痕迹?（不要求写出判断过程）
（2）求出氢核在磁场中运动的轨道半径.
（3）反氢核在MN上留下的痕迹与氢核在MN上留下的痕迹之间的距离是多少?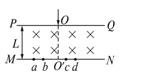

参考答案：（1）由左手定则可判定偏转方向，从而判断出a,b为反粒子，由半径公式R=mv/Bq可确定a、b、c、d四点分别是反氢核、反氦核、氦核和氢核留下的痕迹. （2分）
（2）对氢核，在磁场中做匀速圆周运动，由牛顿第二定律得：
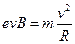?（2分）
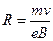得：?（2分）
（3）由图中几何关系知：
?（2分）
所以反氢核与氢核留下的痕迹之间的距离
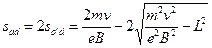?（2分）

本题解析：略

本题难度：简单

5、选择题  如图15-5-7所示，在有界匀强磁场边界线SP∥NM，速度不同的同种带电粒子从S点沿SP方向同时射入磁场，其中穿过a点的粒子速度v1与MN垂直，穿过b点的粒子，其速度方向与MN成60°角.设两粒子从S到a、b所需时间分别为t1、t2，则t1∶t2为（?）

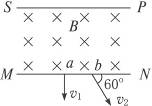
图15-5-7
A．1∶3
B．4∶3
C．1∶1
D．3∶2

参考答案：D

本题解析：根据t=T，T与速度大小无关.
所以t1=
所以t1∶t2=，D正确.

本题难度：简单