1、选择题 如图,两轮用齿轮传动,且不打滑,图中两轮的边缘上有A、B两点,它们的角速度分别为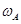 和
和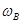 ,线速度大小分别为
,线速度大小分别为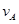 和
和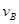 ,到各自转轴O1、O2的距离分别为
,到各自转轴O1、O2的距离分别为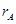 、
、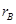 且
且 . 当轮子转动时,这两点则下列关系式正确的是(?)
. 当轮子转动时,这两点则下列关系式正确的是(?)
A、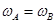 ? B、
? B、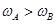 ?
?
C、 ? D、
? D、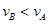
参考答案:C
本题解析:A和B两点相切,所以两个齿轮上的A和B两点的线速度相同,C正确,D错误; ,由
,由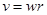 可知
可知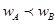 ,所以A和B错误。
,所以A和B错误。
本题难度:简单
2、选择题 关于向心加速度,下列说法正确的是(?)
A.它是描述角速度变化快慢的物理量
B.它是描述线速度大小变化快慢的物理量
C.它是描述线速度方向变化快慢的物理量
D.它是描述角速度方向变化快慢的物理量
参考答案:C
本题解析:从匀速圆周运动的特点入手思考。匀速圆周运动其角速度大小不变,角速度的方向是不变的。线速度方向总是与半径垂直,半径转过多少度,线速度的方向就改变多少度。
本题难度:一般
3、填空题 如图为自行车局部示意图,自行车后轮的小齿轮半径R1=4.0cm,与脚踏板相连的大齿轮的半径R2=10.0cm.则小齿轮边缘处A点的线速度与大齿轮边缘B点的线速度之比v1:v2=______,小齿轮的角速度和大齿轮的角速度之比ω1:ω2=______.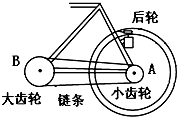
参考答案:传动过程中,同一链条上的A、B两点的线速度相等,即vA=vB
所以v1:v2=1:1
根据ω=vr得:
ω1ω2=v1r2v2r1=?r2?r1=0.10.04=52
所以小齿轮的角速度和大齿轮的角速度之比ω1:ω2=5:2
故答案为:1:1;5:2
本题解析:
本题难度:一般
4、简答题 在圆周运动中定义:质点的角速度变化量跟发生这一变化所用时间的比值叫做角加速度.设一质点正在做角加速度恒定为β的圆周运动,某段时间内质点转过的圆心角为θ,该段时间初时刻的角速度为ω0,试求该段时间末时刻的角速度ω.
参考答案:设某段时间为t,由定义可得β=ω-ω0t
又角速度在均匀增加,所以有θ=ω0+ω2t
消去t可得ω2-ω02=2βθ
解得:ω=
本题解析:
本题难度:一般
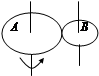
5、填空题 如图所示,A和B为两个紧靠在一起的硬质橡胶轮,两轮的半径之比RA:RB=3:1.A转动时带动B一起转动(转动过程中两轮间无打滑现象),两轮的线速度之比vA:vB=______,两轮的转速之比nA:nB=______.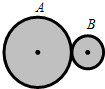
参考答案:传动过程中,皮带不打滑,说明A、B两点的线速度相等,即vA=vB
根据ω=vR 得,ω与R成反比,即为ωA:ωB=1:3,
根据ω=2πn,得n与R成反比,即为nA:nB=1:3;
故答案为:1:1,1:3.
本题解析:
本题难度:一般