1、实验题 如图16-2-4所示,质量为m、长为a的汽车由静止开始从质量为M、长为b的平板车一端行至另一端时,汽车发生的位移大小为_____________,平板车发生的位移大小为_____________(水平面光滑).
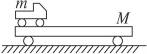
图16-2-4
参考答案: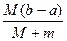 ?
?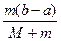
本题解析:系统动量守恒,设汽车位移大小为x,则平板车位移大小为b-a-x.列方程为mx=M(b-a-x),得x=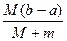 ,b-a-x=
,b-a-x=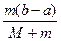 .
.
本题难度:简单
2、计算题 (9分)某些建筑材料可产生放射性气体——氡,氡可以发生α或β衰变,如果人长期生活在氡浓度过高的环境中,那么,氡经过人的呼吸道沉积在肺部,并放出大量的射线,从而危害人体健康。原来静止的氡核( Rn)发生一次α衰变生成新核钋(Po),并放出一个能量为E0=0.09 MeV的光子。已知放出的α粒子动能为Eα=5.55 MeV;忽略放出光子的动量,但考虑其能量;1 u =931.5 MeV/ c2 。
Rn)发生一次α衰变生成新核钋(Po),并放出一个能量为E0=0.09 MeV的光子。已知放出的α粒子动能为Eα=5.55 MeV;忽略放出光子的动量,但考虑其能量;1 u =931.5 MeV/ c2 。
①写出衰变的核反应方程;
②衰变过程中总的质量亏损为多少?(保留三位有效数字)。
参考答案:①?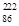 Rn
Rn
 Po+
Po+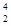 He+γ?②0.006 16 u
He+γ?②0.006 16 u
本题解析:(2)①衰变方程为: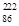 Rn
Rn
 Po+
Po+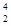 He+γ ;(2分,无γ 不扣分)
He+γ ;(2分,无γ 不扣分)
②忽略放出光子的动量,根据动量守恒定律,0=pα+pPo,(2分)
即新核钋(Po)的动量与α粒子的动量大小相等,又Ek=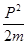 ,(1分)
,(1分)
可求出新核钋(Po)的动能为EPo=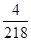 Eα. (1分)
Eα. (1分)
由题意,质量亏损对应的能量以光子的能量和新核、α粒子动能形式出现衰变时释放出的总能量为ΔE=Eα+EPo+E0=Δmc2(2分)
故衰变过程中总的质量亏损是Δm=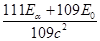 =0.00616u(1分)
=0.00616u(1分)
本题难度:一般
3、计算题 (19分)如图所示,光滑水平面上固定一半径为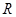 的光滑水平圆形轨道,过圆心
的光滑水平圆形轨道,过圆心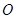 相垂直的两虚线交圆弧于A、B、C、D四点,质量为
相垂直的两虚线交圆弧于A、B、C、D四点,质量为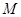 的乙球静置于B处,质量为
的乙球静置于B处,质量为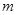 的甲球从A处沿圆弧切线方向以速度
的甲球从A处沿圆弧切线方向以速度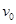 开始运动,到达B处与乙球发生碰撞,碰撞时间很短可忽略不计,碰撞为弹性碰撞,两小球可视为质点.当乙球刚运动到D处时,两小球发生第二次碰撞.求:?
开始运动,到达B处与乙球发生碰撞,碰撞时间很短可忽略不计,碰撞为弹性碰撞,两小球可视为质点.当乙球刚运动到D处时,两小球发生第二次碰撞.求:?
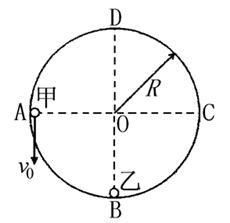
(1)第一次碰撞前甲所受轨道弹力的大小;
(2)甲、乙两球质量之比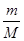 ;
;
(3)甲与乙第二次碰撞后各自速度的大小.
参考答案:(1)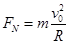 ?(2)
?(2)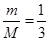 ?(3)
?(3)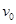 、0
、0
本题解析:
试题分析:(1)甲与乙第一次碰撞前,对甲受力知受重力和轨道的支持力 ,由牛顿第二定律:
,由牛顿第二定律:
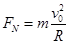 ?(5分)
?(5分)
(2)由题分析知,甲与乙第一次碰撞后必反向运动,速度大小必相等
设甲、乙第一次碰撞后速度大小分别为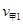 、
、 ,以向右为正方向
,以向右为正方向
有: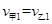 ?(1分)
?(1分)
由动量守恒定律: ?(2分)
?(2分)
由能量守恒定律: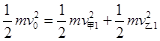 ?(2分)
?(2分)
解得: ?,?
?,?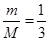 ?(2分)
?(2分)
(3)设甲、乙第二次碰撞后各自速度大小为 、
、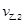 ,
,
由动量守恒定律: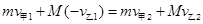 ?(2分)?
?(2分)?
由能量守恒定律: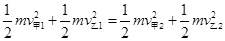 ?(2分)
?(2分)
解得: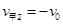 ?
? ?
?
即甲与乙第二次碰撞后各自速度大小分别为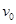 和0?(3分)
和0?(3分)
本题难度:一般
4、选择题 质量为M的原子核,原来处于静止状态。当它以速度v放出质量为m的粒子时(设v的方向为正方向),剩余部分的速度为
A.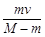
B.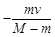
C.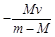
D.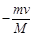
参考答案:B
本题解析:质量为M的原子核,原来处于静止状态。当它以速度v放出质量为m的粒子的过程中动量守恒,设剩余部分的速度为vx,由0=(M-m)vx+mv,得vx=- ,B正确.
,B正确.
本题难度:简单
5、简答题 如图所示,人与冰车质量为M,球质量为m,开始均静止于光滑冰面上,现人将球以对地速度V水平向右推出,球与挡板P碰撞后等速率弹回,人接住球后又将球以同样的速度V向右推出……如此反复,已知M =" 16" m,试问人推球几次后将接不到球?
?
参考答案:9
本题解析:取水平向左为正方向,冰车、人、球为系统.由动量守恒定律,
对第一次推球过程有:?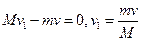
对第二次整个接、推球过程有:
对第三次整个接、推球过程有:
对第n次整个接、推球过程同理分析得: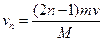 ?
?
设推球n次后恰接不到球,则 ,故有
,故有 ?代人已知条件
?代人已知条件
解得:n = 8.5,?即人推球9次后将接不到球.
本题难度:一般