1、计算题  如图甲所示,空间存在B="0.5" T?方向竖直向下的匀强磁场,MN?PQ是放在同一水平面内的平行长直导轨,其间距L="0.2" m,R是连在导轨一端的电阻,ab是跨接在导轨上质量m="0.1" kg的导体棒.从零时刻开始,对ab施加一个大小为F="0.45" N?方向水平向右的恒定拉力,使其从静止开始沿导轨运动,此过程中棒始终保持与导轨垂直且良好接触,图乙是棒的速度—时间关系图象,其中AO是图象在O点的切线,AB是图象的渐近线.

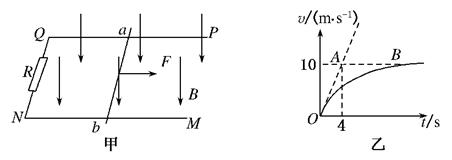
(1)除R以外,其余部分的电阻均不计,求R的阻值;
(2)当棒的位移为100 m时,其速度已经达到10 m/s,求此过程中电阻上产生的热量.

参考答案：(1)0.4 Ω? (2)20 J

本题解析：(1)由图象可知,导体棒刚运动时,加速度a="2.50" m/s2,设它受的摩擦力为f.由牛顿运动定律得
F=f+ma?解得:f="0.2" N
导体棒匀速运动时,由力的平衡得
F=F安+f?且F安=BIL? I=BLv/R
解得:R=B2L2v/(F-f)="0.4" Ω
(2)根据能量守恒得? Fs-fs=mv2/2+Q
解得Q="20" J.

本题难度：一般

2、计算题  一个线圈有100匝、面积为0．01m2，线圈的内电阻为0．5Ω，线圈两端接一个9．5Ω的电阻。线圈在0．02S的时间内从磁感应强度均为0．4T的磁铁两极间移出，
求：（1）线圈的感应电动势多大？
（2）电路中产生的电流多大？
（3）线圈两端的电压多大？

参考答案：（1）20V （ 2）2A（3）19V

本题解析：依题意： （1）线圈中的感应电动势

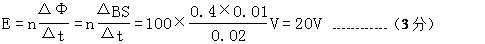
（ 2）电路中产生的电流

（3）线圈两端的电压
?
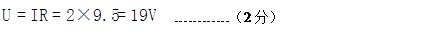本题考查法拉第电磁感应定律的应用，由法拉第电磁感应定律公式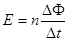先求的电动势大小，其中n为线圈匝数，再由闭合电路欧姆定律E=I(R+r)可求得闭合电路中电流大小，由欧姆定律U=IR可求得线圈两端电压大小

本题难度：一般

3、选择题  线圈在长直导线电流的磁场中，做如图的运动：A向右平动，B向下平动，C绕轴转动(ad边向外)，D从纸面向纸外作平动，E向上平动(E线圈有个缺口)，线圈中有感应电流的是_____(填代号)

参考答案：BCE

本题解析：产生感应电流的条件是通过闭合线圈的磁通量发生变化，所以从图中可得AD磁通量不变，BCE磁通量变化，所以BCE产生感应电流
点评：关键是能够判断图中各种运动里的磁通量是否发生变化

本题难度：简单

4、选择题  如图所示，乙线圈和甲线圈互相绝缘，且乙线圈有一半面积在甲线圈内，当甲线圈中的电流逐渐减弱时，乙线圈中的感应电流?

A．为零
B．顺时针流动
C．逆时针流动
D．无法确定

参考答案：B

本题解析：乙线圈中磁场方向向里，因为甲线圈中的电流逐渐减弱根据“增反减同”可知乙线圈中会产生向里的感应场，则感应电流方向为顺时针，选B

本题难度：简单

5、简答题  高频焊接是一种常用的焊接方法，图1是焊接的原理示意图．将半径为r=10cm的待焊接的环形金属工件放在线圈中，然后在线圈中通以高频变化电流，线圈产生垂直于工件所在平面的匀强磁场，磁感应强度B随时间t的变化规律如图2所示，t=0时刻磁场方向垂直线圈所在平面向外．工件非焊接部分单位长度上的电阻R0=1.0×10-3Ω?m-1，焊缝处的接触电阻为工件非焊接部分电阻的9倍，焊接的缝宽非常小，不计温度变化对电阻的影响．

（1）求环形金属工件中感应电流的大小，在图3中画出感应电流随时间变化的i-t图象（以逆时针方向电流为正）；

参考答案：（1）环形金属工件电阻为R=2πrR0+9×2πrR0=20πrR0=6.28×10-3Ω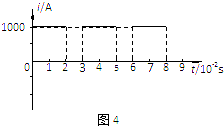
在0-23T时间内的感应电动势为E=△B△t?πr2=6.28V
电流为I=ER=1.0×103A
由楞次定律得到电流方向逆时针
I-t关系图象如图所示．
（2）设环形金属工件中电流的有效值为I效，在一个周期内
I效2RT=I2R2T3
解得：I效=1000

本题解析：

本题难度：一般