参考答案：工件受到的摩擦力产生的加速度a=μg=0.2×10=2m/s2；
则其速度到达6m/s时的位移x=v22a=362×2=9m＜10m；故物体到达B点时的速度已达到最大速度；
由动能定理可知：W=12mv2=12×1×36=18J；
故选：C．

本题解析：

本题难度：简单

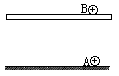
2、计算题  如图所示，A、B是两个带正电的点电荷，电荷量均为q，A固定在绝缘物体上，在它正上方的B则放在一块绝缘板上。现用手握着绝缘板从静止起加以加速度a竖直向下做匀加速运动（a＜g），若B的质量为m，静电力常量为k，A、B之间的作用力按真空条件处理。问：
(1)B运动到离A多远的C处将会脱离绝缘板？
(2)若BC=2CA，则在以上的运动过程中，电场力和绝缘板的支持力对B做功的代数和等于多少？

参考答案：解：（1）设B运动到离A的距离为r处时刚好脱离绝缘板，对B由牛顿第二定律，有：
mg--N=ma
当N=0时，r=
（2）设电场力和支持力做功的代数和为W，则由动能定理可得：
mg×2r+W=
又v2=2a×2r
联立解得：W=

本题解析：

本题难度：一般

3、简答题  如图所示，宽为L=0.5m、足够长的平行金属导轨MN和M’N’固定在倾角为θ=37°的斜面上，在N和N’之间连有一个0.8Ω的电阻R．在导轨上AA’处放置一根与导轨垂直、质量为m=0.2kg、电阻r=0.2Ω的金属棒，导轨电阻均不计．在导轨所围的区域存在一个磁感应强度B=2.0T、方向垂直于斜面向上的匀强磁场，已知金属棒和导轨间的动摩擦因数为μ=0.25．现在金属棒中点施加一个垂直于金属棒且沿斜面向上的外力F，使金属棒从静止开始以加速度a=lm/s2沿斜面向上做匀加速直线运动，经3s恰好经过CC‘处．求：
（1）金属棒从AA‘运动到CC‘过程中通过R的电荷量；
（2）金属棒通过CC‘时所施加的外力F的大小；
（3）如果在此过程中外力F所做的功为17.1J，求在此过程中金属棒放出的焦耳热是多少？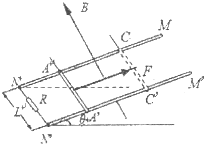

参考答案：（1）金属棒从AA′开始做匀加速运动的过程中，其位移为：
x=12at2=12×1××32m=4.5m
由：.E=△Φ△t、.I=.ER+r、q=.I?△t
得电量：q=BLxR+r=2×0.5×4.50.8+0.2C=4.5C．
（2）金属棒运动到CC′时：
v=at=3m/s
感应电动势：E=BLv，I=ER+r=BLatR+r
根据牛顿第二定律得：
F-mgsinθ-μmgcosθ-BIL=ma
解得，F=4.8N
（3）在此过程中，对金属棒运用动能定理得：
W-mgsinθ?x-μmgcosθ?x-W安=12mv2
解得：Q=W安=9J
根据焦耳定律得知，金属棒放出的焦耳热为：
Qr=rr+RQ=1.8J
答：（1）从AA‘运动到CC‘过程中通过R的电荷量是4.5C；
（2）金属棒通过CC′时所施加的外力F的大小是4.8N；
（3）金属棒放出的焦耳热为1.8J．

本题解析：

本题难度：一般

4、选择题  质量为m的物体，由静止开始下落，由于阻力作用，下落的加速度为4g/5，在物体下落h的过程中，下列说法中正确的是：（?）
A．物体的动能增加了4mgh/5
B．物体的机械能减少了4mgh/5
C．物体克服阻力所做的功为mgh/5
D．物体的重力势能减少了mgh

参考答案：ACD

本题解析：物体的合外力为，下降了h，所以根据动能定理得物体的动能增加了4mgh/5，物体的重力势能减小了mgh，克服阻力做功，机械能减小了，所以ACD正确。

本题难度：简单

5、简答题  如图所示，将半径为r的

参考答案：（1）小球从A滑到B的过程中，由动能定理得：
mgr=12mvB2-0，
解得：vB=

本题解析：

本题难度：一般