1、计算题 一名宇航员抵达一半径为R的星球表面后，为了测定该星球的质量，做了如下实验：将一个小球从该星球表面某位置以初速度v竖直向上抛出，小球在空中运动一段时间后又落回原抛出位置，测得小球在空中运动的时间为t，已知万有引力恒量为G，不计阻力。试根据题中所提供的条件和测量结果，求：
（1）该星球表面的“重力”加速度g的大小；
（2）该星球的质量M；
（3）如果在该星球上发射一颗围绕该星球做匀速圆周运动的卫星，则该卫星运行的最小周期T为多大？
参考答案：解：（1）由运动学公式得：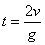
解得该星球表面的“重力”加速度的大小
（2）质量为m的物体在该星球表面上受到的万有引力近似等于物体受到的重力，则对该星球表面上的物体，由牛顿第二定律和万有引力定律得：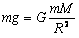
解得该星球的质量为
（3）当某个质量为m′的卫星做匀速圆周运动的半径等于该星球的半径R时，该卫星运行的周期T最小，则由牛顿第二定律和万有引力定律：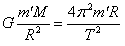
解得该卫星运行的最小周期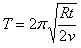
本题解析：
本题难度：一般
2、选择题 已知天宫一号绕地球做圆周运动的半径为r，周期为T，万有引力常量为G，由此可求出（ ）
A．天宫一号的线速度
B．天宫一号所需向心力
C．地球的质量
D．地球表面的重力加速度
参考答案：
A、根据v=2πrT可得线速度的大小；
B、因为不知道天宫一号的质量，故无法求出天宫一号所需的向心力；
C、根据GmMr2=mr4π2T2?M=4π2r3GT2，故C正确；
D、因为不知道地球的半径，故无法算出地球表面的重力加速度．
故选AC．
本题解析：
本题难度：简单
3、选择题 地球的质量为M，半径为R，自转角速度为ω，万有引力常量为G，地球表面的重力加速度为g，同步卫星距地面的距离为h，则同步卫星的线速度大小为（ ）
A．ω（R+h）
B．
C．R
D．
参考答案：同步卫星与地球同步，做匀速圆周运动，则线速度定义可得：
v=2πrT=2π(R+h)2πω=ω(R+h)
由于地球的引力提供向心力，让同步卫星做匀速圆周运动，则有：
GMm(R+h)2=mv2R+h
解之得：v=
本题解析：
本题难度：简单
4、选择题 关于同步卫星，正确的说法是（? ）
A．可以定点在雅安中学上空
B．它运行的线速度一定小于第一宇宙速度
C．各国发射的同步卫星线速度大小、角速度、周期、轨道半径都一样
D．发射同步卫星的速度必须大于第一宇宙速度
参考答案：BC
本题解析：同步卫星只能位于赤道正上方的某一高度，A错误，由线速度公式 可知，半径越大，速度越小，同步卫星的运动半径大于近地卫星的运动半径，所以同步卫星的线速度小于第一宇宙速度，B正确，因为同步卫星的角速度和地球自转的角速度相同，根据 可得半径相同，根据， ，都是相同的，C正确；发射速度大于第一宇宙速度，将逃离地球，称为其他星体的卫星，D错误
故选BC
点评：同步卫星有四个“定”：定轨道、定高度、定速度、定周期．本题难度不大，属于基础题．
本题难度：一般
5、选择题 欧盟和我国合作的“伽利略”全球定位系统的空间部分由平均分布在三个轨道面上的30颗轨道卫星组成，每个轨道平面上等间距部署10颗卫星，从而实现高精度的导航定位，现假设“伽利略”系统中每颗卫星均绕地心O做匀速圆周运动，一个轨道平面上某时刻10颗卫星所在位置分布如图所示。若卫星均顺时针运行，地球表面处的重力加速度为g，不计卫星间的相互作用力。
则以下判断中正确的是
A．这些卫星的运行速度均小于7.9km/s
B．这些卫星的加速度大小均小于g
C．这些卫星处于完全失重状态
D．若已知这些卫星的周期和轨道半径，可求出卫星的质量
参考答案：ABC
本题解析：根据万有引力提供向心力可得： ，7.9km/s是第一宇宙速度，也是最大环绕速度，故这些卫星的运行速度均小于7.9km/s，故A正确
根据万有引力提供向心力可得： ，因为轨道半径大于地球半径，所以.这些卫星的加速度大小均小于g，故B正确
由于根据万有引力提供向心力，故这些卫星处于完全失重状态，故C正确
若已知这些卫星的周期和轨道半径，可求出中心天体（即地球）的质量，卫星的质量在等量两边被消掉，故不可求得，故D错误
故选：ABC
本题难度：一般
If money be not the servant,it will be the master. 不做金钱的主人,便沦为金钱的奴隶. |
|
考试问吧
