D.小球运动的线速度v=
参考答案:A、由a=ω2R,得到ω=
本题解析:
本题难度:一般
2、计算题 一部机器由电动机带动,机器上的皮带轮的半径是电动机皮带轮半径的3倍(如图),皮带与两轮之间不发生滑动。已知机器皮带轮边缘上一点的向心加速度为0.10 m/s2。
(1)电动机皮带轮与机器皮带轮的角速度之比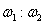 =? =?
(2)机器皮带轮上A点到转轴的距离为轮半径的一半,A点的向心加速度是多少?
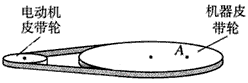
参考答案:解:(1)因电动机和机器由同一皮带连接,所以它们边缘线速度相等。设电动机半径为r1,角速度ω1,机器轮半径为r2,角速度为ω2
由题意知:r2=3r1
由v=rω得r1ω1=r2ω2
即r1ω1=3r1ω2
所以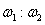 =3:1 =3:1
(2)因A与皮带边缘同轴转动,所以角速度相等,向心加速度与半径成正比
由a=rω2得aA=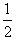 ×0.10 m/s2 =0.05 m/s2 ×0.10 m/s2 =0.05 m/s2
本题解析:
本题难度:一般
3、实验题 一个有一定厚度的圆盘,可以绕通过中心垂直于盘面的水平轴转动,用下面的方法测量它匀速转动时的角速度。
实验器材:交流电源(频率为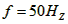 ),电磁打点计时器,米尺,纸带,复写纸。 ),电磁打点计时器,米尺,纸带,复写纸。
实验步骤:
①如图甲所示,将电磁打点计时器固定在桌面上,将纸带的一端穿过打点计时器的限位孔后固定在待测圆盘的侧面上,使圆盘转动时,纸带可以卷在圆盘侧面上。
②启动控制装置使圆盘转动,同时接通电源,打点计时器开始打点。
③经这一段时间后,停止转动和打点,取下纸带,进行测量。

(1)由已知量和测得量表示角速度ω的表达式为__________,式中各量的意义是__________。
(2)某次实验测量圆盘半径5.5×10-2m ,得到纸带的一段如图乙所示,求得角速度为___________。

参考答案:(1)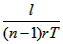 , , 表示纸带上某两点间的距离,r表示待测圆盘的半径,T表示打点的时间间隔,n表示所打的点数。 表示纸带上某两点间的距离,r表示待测圆盘的半径,T表示打点的时间间隔,n表示所打的点数。
(2)6.82rad/s
本题解析:
本题难度:一般
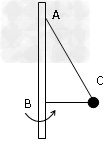
4、计算题 如图所示AB 为竖直转轴,细绳AC 和BC 的结点C 系一质量为m的小球,两绳能承担的最大拉力均为2.25mg,当AC和BC均拉直时∠ABC=90°,∠ACB=53°,BC=1.2m。ABC能绕竖直轴AB匀速转动,因而C球在水平面内做匀速圆周运动,求:(g取10m/s2)
(1) m的线速度增大为何值时,BC绳才刚好被拉直?
(2)若m的速率继续增加,哪条绳先断,此时小球的速率多大?
参考答案:(1 )3m/s?
(2 )BC 绳先断;6m/s
本题解析:
本题难度:一般
5、实验题 如图甲所示为测量电动机转动角速度的实验装置,半径不大的圆形卡纸固定在电动机转轴上,在电动机的带动下匀速转动。在圆形卡纸的旁边垂直安装一个改装了的电火花计时器。

(1)请将下列实验步骤按先后排序:___________________。
A.使电火花计时器与圆形卡纸保持良好接触
B.接通电火花计时器的电源,使它工作起来
C.启动电动机,使圆形卡纸转动起来
D.关闭电动机,拆除电火花计时器;研究卡纸上留下的一段痕迹(如图乙所示),写出角速度ω的表达式,代入数据,得出ω的测量值。
(2)要得到ω的测量值,还缺少一种必要的测量工具,它是____________。
A.秒表
B.毫米刻度尺
C.圆规
D.量角器
(3)写出角速度ω的表达式,并指出表达式中各个物理量的意义:_______________。
参考答案:(1)A、C、B、D
(2)D
(3)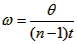 (θ为n个点对应的圆心角,t为时间间隔) (θ为n个点对应的圆心角,t为时间间隔)
本题解析:
本题难度:困难
|