1、计算题 利用如图所示装置可调控带电粒子的运动,通过改变左端粒子入射速度的大小,可以控制粒子到达右端接收屏上的位置,装置的上下两个相同的矩形区域内存在匀强磁场,磁感应强度大小均为B、方向与纸面垂直且相反,磁场区域的宽度均为h,磁场区域长均为15h,P、Q为接收屏上的二点,P位于轴线 上,Q位于下方磁场的下边界上。在纸面内,质量为m、电荷量为+q的粒子以某一速度从装置左端的中点射入,方向与轴线成370角,经过上方的磁场区域一次,恰好到达Q点。不计粒子的重力 (sin370=0.6、cos370=0.8)。问:
上,Q位于下方磁场的下边界上。在纸面内,质量为m、电荷量为+q的粒子以某一速度从装置左端的中点射入,方向与轴线成370角,经过上方的磁场区域一次,恰好到达Q点。不计粒子的重力 (sin370=0.6、cos370=0.8)。问:
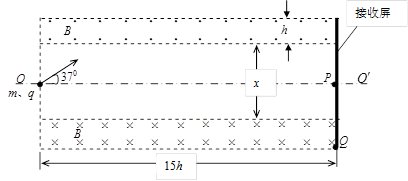
(1)上下两磁场间距x为多少?
(2)仅改变入射粒子的速度大小,使粒子能打到屏上P点,求此情况下入射速度大小的所有可能值。
参考答案:(1)3h(2)
本题解析:(1)设粒子磁场中圆周运动半径为R
15h=3Rsin37°+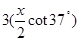
h=R(1-cos37°)
得x=3h
(2)一情况:设粒子经过上方磁场n次,下方磁场n次后到达P点,
由题意可知:15h=4n( +4nRNsin37°
+4nRNsin37°
解得: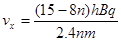
讨论:又15-8n>0,即n<15/8 故 n=1, 
另一情况:经过上方磁场n次,下方磁场n-1次后到达P点
15h=(4n-2)( +(4n-2)RNsin37°
+(4n-2)RNsin37°

 由于粒子经过上方的磁场区域一次,恰好到达Q点,因此粒子不可能只经过上方一次射出后直接到达P点,因此有:n≥2 与19-8n>0得n=2。故只有一解:
由于粒子经过上方的磁场区域一次,恰好到达Q点,因此粒子不可能只经过上方一次射出后直接到达P点,因此有:n≥2 与19-8n>0得n=2。故只有一解:  不讨论,直接得结果不给分。
不讨论,直接得结果不给分。
考点:带电粒子在匀强磁场中的运动;动能定理.
本题难度:困难
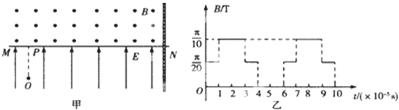
2、简答题 如图甲所示,水平直线MN下方有竖直向上的匀强电场,场强E=
×104N/C.现将一重力不计、比荷=106C/kg的正电荷从电场中的O点由静止释放,经过t0=1×10-5s后,通过MN上的P点进入其上方的匀强磁场.磁场方向垂直于纸面向外,以电荷第一次通过MN时开始计时,磁感应强度按图乙所示规律周期性变化.
(1)求电荷进入磁场时的速度v0;
(2)求图乙中t=2×10-5s时刻电荷与P点的距离;
(3)如果在P点右方d=105cm处有一垂直于MN的足够大的挡板,求电荷从O点出发运动到挡板所需的时间.
参考答案:(1)电荷在电场中做匀加速直线运动,设其在电场中运动的时间为t1,有:
v0=at0 Eq=ma
解得:v0=qEm?t0=qm?Et0=106×π10×104×1×10-5m/s=π×104m/s;
(2)当磁场垂直纸面向外B1=π20T时,电荷运动的半径:r1=mv0qB1
代入数据得:r1=0.2m
周期T1=2πmqB1
代入数据得:T1=4×10-5s
当磁场B2=π10时,电荷运动的半径:r2=mv0qB2
代入数据得:r2=0.1m
周期T2=2πmqB2
代入数据得:T2=2×10-5s
故电荷从t=0时刻开始做周期性运动,其运动轨迹如图1所示.
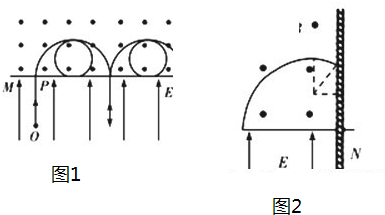
t=2×10-5s时刻电荷先沿大圆轨迹运动四分之一周期,然后再沿小圆弧运动半个周期,与P点的水平距离:△d=r1=0.2m;
(3)电荷从第一次通过MN开始,其运动的周期为:T=6×10-5 s,每一个周期内沿PN的方向运动的距离为0.4=40cm,故电荷到达挡板前运动的完整的周期数为2个,沿PN方向运动的距离为80cm,最后25cm的距离如图2所示,设正电荷以α角撞击到挡板上,有:
r1+r2cosα=0.25m
代入数据解得:cosα=0.5,即α=60°
故电荷运动的总时间:t总=t0+2T+14T1+30°360°?T2
代入数据解得:t总=1.42×10-5s
答:(1)电荷进入磁场时的速度为π×104m/s.(2)t=2×10-5s时刻电荷与P点的水平距离为20cm.(3)电荷从O点出发运动到挡板所需的时间为1.42×10-4s.
本题解析:
本题难度:一般
3、计算题 如图甲所示,两平行金属板间接有如图乙所示的随时间t变化的电压UAB,两板间电场可看做是均匀的,且两板外无电场,极板长L=0.2m,板间距离d=0.2m,在金属板右侧有一边界为MN的区域足够大的匀强磁场,MN与两板间中线OO′垂直,磁感应强度B=5×10-3 T,方向垂直纸面向里。现有带正电的粒子流沿两板中线OO′连续射入电场中,已知每个粒子的速度v0=105m/s,比荷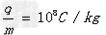 ,重力忽略不计,每个粒子通过电场区域的时间极短,此极短时间内电场可视作是恒定不变的。求:?
,重力忽略不计,每个粒子通过电场区域的时间极短,此极短时间内电场可视作是恒定不变的。求:?
(1)在t=0.1s时刻射入电场的带电粒子,进入磁场时在MN上的入射点和出磁场时在MN上的出射点间的距离为多少;?
(2)带电粒子射出电场时的最大速度;?
(3)在t=0.25s时刻从电场射出的带电粒子,在磁场中运动的时间。
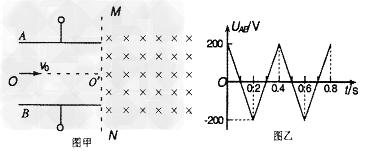
参考答案:解:(1)在 时刻射入电场的带电粒子,在极板间做匀速直线运动,以v0垂直磁场边界垂直射入磁场,由
时刻射入电场的带电粒子,在极板间做匀速直线运动,以v0垂直磁场边界垂直射入磁场,由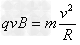 可得:
可得: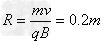
在MN上的入射点和出磁场时在MN上的出射点间的距离为: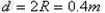
(2)设带电粒子从极板的边缘射出电场时的速度最大,对应的瞬时电压为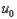 ,则:
,则:

解得: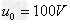
由动能定理:
射出的最大速度
(3)在 时刻从电场射出的带电粒子,从极板的上边缘射出电场,垂直进入磁场时与磁场边界的夹角为
时刻从电场射出的带电粒子,从极板的上边缘射出电场,垂直进入磁场时与磁场边界的夹角为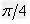 ,射出磁场时与磁场边界的夹角也为
,射出磁场时与磁场边界的夹角也为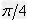 ,故对应的圆周的圆心角为
,故对应的圆周的圆心角为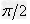 ,故在磁场中运动的时间为圆周运动周期的四分之一
,故在磁场中运动的时间为圆周运动周期的四分之一
由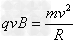 ,
,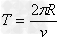
得到: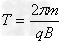 ,所以
,所以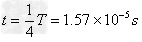
本题解析:
本题难度:一般
4、简答题 如图所示,半径为r=0.10m的圆形匀强磁场区域边界跟x轴相切于坐标原点O,磁感应强度按图示规律变化,方向垂直直纸面向里,在t=0时刻由O处沿y轴正方向射入速度为v=1.0×103m/s的带负电粒子,已知粒子质量m=9.0×10-12kg,电量q=9.0×10-6C,不计粒子重力,求粒子在磁场中的运动时间和离开磁场时的位置坐标.
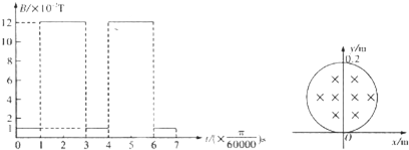
参考答案:粒子进入磁场后,由洛伦兹力提供向心力,做匀速圆周运动,设单位时间t=π6×10-4s.则
在第一个t内,B1=1×10-2T
由qvB1=mv2R1
得,R1=mvqB1=0.1m
T1=2πmqB1=2π×10-4s
故t=112T1
则粒子在第一个t内,在磁场中转过的圆心角为30°.
在第二个t内,B2=12×10-2T
T2=2πmqB2=π6×10-4s
则t=T2,
故粒子在第二个和第三t内刚好做两个完整的圆周运动,第四个t内的运动与第一t内的相同,第五、六个t内的运动又与第二、第三个t内的相同,到第七个t末,粒子刚好出磁场,
由上分析可知,粒子在磁场中运动时间为
t′=7t=76π×10-4s,运动轨迹如图,离开磁场时的位置坐标为(0.1,0.1)
答:粒子在磁场中的运动时间是76π×10-4s,离开磁场时的位置坐标为(0.1,0.1).
本题解析:
本题难度:一般
5、选择题 比荷为e/m的电子以速度v0。沿AB边射人边长为a的等边三角形的匀强磁场区域中,如图所示,为使电子从BC边穿出磁场,磁感应强度B的取值范围为( ? )

A.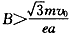
B.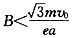
C.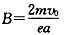
D.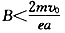
参考答案:B
本题解析:
本题难度:一般
Life is short and time is swift. 生命短暂,光阴飞逝.