1、实验题 有一个底面直径和高都是d的空圆筒,眼在A处恰好能看到底圆跟侧壁的交点B,如图所示.现将某种液体注满圆筒,在A处沿原方向看去,能看到底圆的中心C.则这种液体的折射率为____________.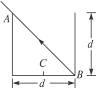
参考答案: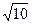 /2
/2
本题解析:当倒入液体时折射率n=sini/sinr=(d/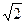 d)/(
d)/(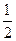 d/
d/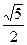 d)=
d)= 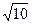 /2.
/2.
本题难度:简单
2、计算题 一底面半径为R的半圆柱形透明体的折射率为 ,横截面如图所示,O表示半圆柱形截面的圆心。一束极窄的光线在横截面内从AOB边上的A点以60°的入射角入射,求:该光线从进入透明体到第一次离开透明体时,共经历的时间(已知真空中的光速为c,
,横截面如图所示,O表示半圆柱形截面的圆心。一束极窄的光线在横截面内从AOB边上的A点以60°的入射角入射,求:该光线从进入透明体到第一次离开透明体时,共经历的时间(已知真空中的光速为c, ;计算结果用R、n、c表示)。
;计算结果用R、n、c表示)。

参考答案:解:设此透明物体的临界角为C
依题意 ,所以
,所以
当入射角为 时,由
时,由
得到折射角:

即此时光线折射后射到圆弧上的C点,在C点的入射角为60°,大于临界角,会发生全反射往后光线水平反射至圆弧上的D点并在D点发生全反射,再反射至B点,从B点第一次射出
在透明体内的路径长为:s=3R?
光在透明体内的速度
经历的时间
本题解析:
本题难度:一般
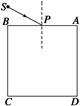
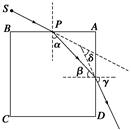
3、计算题 (10分)在真空中有一正方体玻璃砖,其截面如图所示,已知它的边长为d.在AB面上方有一单色点光源S,从S发出的光线SP以60°入射角从AB面中点射入,当它从侧面AD射出时,出射光线偏离入射光线SP的偏向角为30°,若光从光源S到AB面上P点的传播时间和它在玻璃砖中传播的时间相等,求点光源S到P点的距离。
参考答案:L=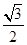 d(
d(
本题解析:(10分)光路图如图所示,由折射定律知,光线在AB面上折射时有n= (1分)
(1分)
在BC面上出射时n=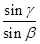 (1分)
(1分)
由几何关系有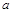 +β=90°(1分)
+β=90°(1分)
δ=(60°-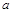 )+(γ-β)=30°(1分)
)+(γ-β)=30°(1分)
联立以上各式并代入数据解得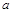 =β=45°,γ=60°(1分)
=β=45°,γ=60°(1分)
所以n=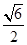 (1分)
(1分)
光在棱镜中通过的距离s= d=
d=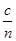 t(2分)
t(2分)
设点光源到P点的距离为L,有L=ct(1分)
解得L=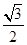 d(1分)
d(1分)
本题难度:一般
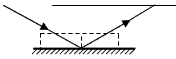
4、计算题 如图所示,一束光线以60°的入射角射到一水平放置的平面镜上,反射后在上方与平面镜平行的光屏上留下一光点P,现在将一块上下两面平行的透明体平放在平面镜上,则进入透明体的光线经平面镜反射后再从透明体的上表面射出,打在光屏上的P′点,与原来相比向左平移了3.46 cm,若透明体对光的折射率为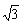 。求光在透明体里运动的时间。
。求光在透明体里运动的时间。
参考答案:2×10-10 s
本题解析:
本题难度:困难
5、简答题 如图所示,一个半径为R的
透明球体放置在水平面上,一束蓝光从A点沿水平方向射入球体后经B点射出,最后射到水平面上的C点.已知OA=,该球体对蓝光的折射率为.则它从球面射出时的出射角β=______;若换用一束红光同样从A点射向该球体,则它从球体射出后落到水平面上形成的光点与C点相比,位置______(填“偏左”、“偏右”或“不变”).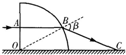
参考答案:根据几何关系得,入射角α=30°.
根据折射定律得,n=sinβsinα=
本题解析:
本题难度:一般