1、计算题  （10分）如图所示，在长为L=57cm的一端封闭、另一端开口向上的竖直玻璃管内，用4cm高的水银柱封闭着51cm长的理想气体，管内外气体的温度均为33℃ ，大气压强p0=76cmHg.

①若缓慢对玻璃管加热，当水银柱上表面与管口刚好相平时，求管中气体的温度；
②若保持管内温度始终为33℃，现将水银缓慢注入管中，直到水银柱上表面与管口相平，求此时管中气体的压强。

参考答案：（1）T2=318K   （2）P2=85cmHg

本题解析：①设玻璃管横截面积为S，以管内封闭气体为研究对象， 气体经等压膨胀：
初状态：  
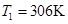
末状态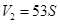：                         （1分）
由盖—吕萨克定律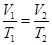：（2分） 得T2=318K   （1分）
②当水银柱上表面与管口相平，设此时管中气体压强为P，水银柱的高度为H，管内气体经等温压缩：
初状态：V1=51S   P1= 80cmHg  （1分）
末状态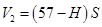：  （1分）
由玻意耳定律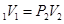：（2分）
得 H=9cm（1分）
故P2=85cmHg（1分）
考点：本题考查盖—吕萨克定律和玻意耳定律。

本题难度：一般

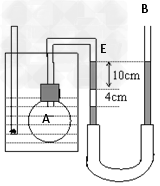
2、计算题  如图所示为验证查理定律的实验装置。A为烧瓶，内贮空气。B为U形管，下部与较长的软橡胶管相连。由于组装不慎，U形管左侧10cm水银柱的下方混入一段长为4cm的空气柱，左侧水银柱上表面与标志线E对齐。开始时烧瓶所在水槽内水温为7℃，U形管两边水银面相平。当水温升至63℃时，调整右边开口水银管的高度，使左侧水银柱上表面仍与标志线E对齐。已知大气压p0=76cmHg。此时?
（1）烧瓶A中的气体压强为多少？
（2）左侧管内空气柱变为多长？?
（3）右侧管内水银面高度将升高多少？

参考答案：解：（1）设烧瓶内空气为A，U形管中混入的空气柱为B，它们初始状态的压强分别为pA和 pB
由图得pB=p0+ρgh=（76+14）cmHg=90cmHg?
pA=pB-ρgh=（90-10）cmHg=80cmHg?
（2）烧瓶内空气为等容变化，设其末状态压强为pA′?

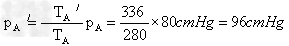
空气柱末状态压强为pB′?
pB′= pA′+ρgh=（96+10）cmHg=106cmHg
空气柱为等温变化，后来长度为LA′?
由pA LA=pA′LA′，得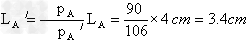
（3）在末状态时，设右管中水银面比原来升高x
则pB′=p0+ρgx+ρgh+ρgLA′?
即106=76+x+10+3.5?
所以x=16.6cm

本题解析：

本题难度：一般

3、计算题  汽车行驶时轮胎的胎压太高容易造成爆胎事故，太低又会造成耗油上升。已知某型号轮胎能在-40℃~90℃正常工作，为使轮胎在此温度范围内工作时的最高胎压不超过3.5atm，最低胎压不低于1.6atm，那么在t=20℃时给该轮胎充气，充气后的胎压在什么范围内比较合适？（设轮胎容积不变）

参考答案：解：由于轮胎容积不变，轮胎内气体做等容变化。设在T0=293K充气后的最小胎压为pmin，最大胎压为pmax
依题意，当T1=233K时胎压为p1=1.6atm
根据查理定律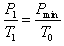，即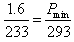，解得：pmin=2.01atm
当T2=363K时胎压为p2=3.5atm
根据查理定律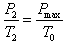，即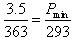，解得：pmax=2.83atm

本题解析：

本题难度：一般

4、简答题  一定质量的理想气体从状态a经历了温度缓慢升高到状态d的变化，下面的表格和V-T图各记录了其部分变化过程，试求：
（1）温度325K时气体的压强．
（2）温度250K时气体的体积．
状态
a
b
压强p/Pa
0.75×105
0.90×105
温度T/K
250
300