1、选择题  如右图所示是用以说明向心力和质量、半径之间关系的仪器，球p和q可以在光滑水平杆上无摩擦地滑动，两球之间用一条轻绳连接，mp＝2mq，当整个装置绕中心轴以角速度ω匀速旋转时，两球离转轴的距离保持不变，则此时(? )?
?
A．两球均受到重力、支持力、拉力和向心力四个力的作用?
B．p球受到的向心力大于q球受到的向心力?

参考答案：C

本题解析：略

本题难度：简单

2、填空题  无极变速可以在变速范围内连续地变换速度，性能优于传统的档位变速器，很多汽车都应用了无极变速．如图所示，是截锥式无极变速模型的示意图，两个锥轮之间有一个滚动轮，主动轮、滚动轮、从动轮之间靠着彼此之间的摩擦力带动．设主动轮转速恒定，当滚动轮从左向右移动时，从动轮转速将增加．当滚动轮位于某位置时，对应的主动轮直径为D1，从动轮直径为D2；当时主动轮转速n1和从动轮转速n2之间的关系是?n1：n2=______．

参考答案：主动轮、滚动轮、从动轮之间是没有打滑的摩擦传动，故它们的轮缘上的线速度大小相等．设主动轮的角速度为ω1，从动轮的角速度为ω2，根据v=ωr，有ω1ω2=r2r1=D2D1．
又因为n1n2=ω1ω2，所以n1n2=D2D1．
故答案为D2：D1

本题解析：

本题难度：一般

3、填空题  质量为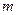的汽车以的速度安全驶过半径为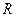的凸形桥的桥顶，这时汽车对桥顶的压力是_________，汽车此时所需的向心力是汽车所受支持力和__________的合力，汽车能安全通过桥顶的最大行驶速度不能超过_____________ (重力加速度为g)

参考答案：；重力?；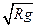

本题解析：略

本题难度：简单

4、选择题  甲、乙两名溜冰运动员质量分别为m甲=80kg和m乙=40kg，面对面拉着一弹簧秤做圆周运动的溜冰表演，如图示，两人相距0.9m，弹簧秤的示数为9.2N，则两人（?）

A．速度大小相同约为40m/s；
B．运动半径分别为r甲=0.3m和r乙=0.6m；
C．角速度相同为6rad/s；
D．运动速率之比为υ甲:υ乙=2:1；

参考答案：B

本题解析：溜冰运动员具有相同的角速度，大小相等的向心力，根据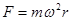，可知运动半径与质量成反比，即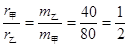，所以r甲=，
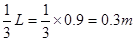r乙=0.9-0.3=0.6m，角速度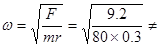6rad/s，运动速率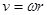可知，速率与半径正比，即υ甲:υ乙=1:2，综合可知只有B正确
故选B

本题难度：一般

5、简答题  在图1所示区域（图中直角坐标系Oxy的1、3象限）内有匀强磁场，磁感强度方向垂直于图面向里，大小为B．半径为l、圆心角为60°的扇形导线框OPQ以角速度ω绕O点在图面内沿逆时针方向匀速转动，导线框回路电阻为R．

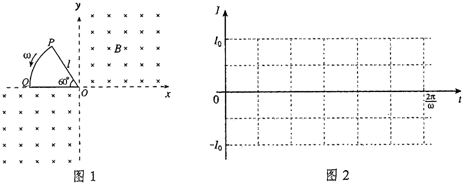
（1）求线框中感应电流的最大值I0和交变感应电流的频率f．
（2）在图2上画出线框转一周的时间内感应电流I随时间t变化的图象（规定与图1中线框的位置相应的时刻为t=0）

参考答案：（1）在从图1中位置开始t=0转过60°的过程中，经△t，转角△θ=ω△t，回路的磁通增量为
△Φ=12△θ?l2B
由法拉第电磁感应定律，感应电动势为：ε=△Φ△t
因匀速转动，这就是最大的感应电动势．由欧姆定律可求得：
I0=12RωBl2
前半圈和后半圈I（t）相同，故感应电流周期为：T=πω，
频率为：f=1T=ωπ．
故感应电流的最大值为I0=12RωBl2，频率为f=ωπ．
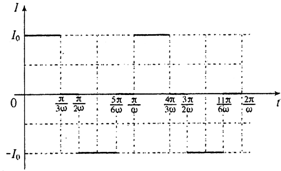
（2）由题可知当线框开始转动π3过程中，有感应电流产生，全部进入时，无感应电流，故当线框全部进入磁场接着再旋转π6过程中无电流，然后出磁场时，又有感应电流产生．
故图线如图所示：

本题解析：

本题难度：一般