1、计算题  在桌面上有一个倒立的透明的玻璃圆锥，其顶点恰好与桌面接触，圆锥的轴（图中虚线）与桌面垂直，过轴线的截面为等边三角形，如图所示。有一半径为r的圆柱形平行光束垂直入射到圆锥的桌面上，光束的中心轴与圆锥的轴重合。已知玻璃的折射率为n=1.73。r为已知，求：
.
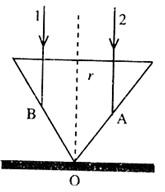
（1）通过计算说明光线1能不能在圆锥的侧面B点发生全反射？
（2）光线1经过圆锥侧面B点后射到桌面上某一点所用的总时间是t多少？光照亮地面的光斑面积s多大？

参考答案：（1）能（2）S=4πr2

本题解析：①（5分）sinC=l/n?（2分）
C=arcsin/3?（1分）
arcsin/2=60°?（2分）
所以光线l能在圆锥的侧面B点发生全反射（1分）

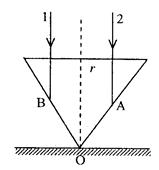
②（5分）根据集合关系知BE=EF=r?（2分）
所以，总时间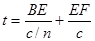?（1分）
=2.73r/c?（2分）
S=4πr2?（1分）
点评：关键之处是借助于光的折射与反射定律作出光路图，同时利用几何关系来辅助计算．

本题难度：一般

2、简答题  在用插针法测定玻璃砖折射率的实验中，
（1）某同学由于没有量角器，在完成了光路以后，他以O点为圆心、10.00cm长为半径画圆，分别交线段OA于A点，交OO′连线延长线于C点，过A点作法线NN′的垂线AB交NN′于点B，过C点作法线NN′的垂线CD交NN′于D点，如图1所示．用刻度尺量得OB=8.00cm，CD=4.00cm．由此可得出玻璃的折射率n=______．
（2）某同学在纸上画出的界面aa′、bb′与玻璃砖位置的关系如图2所示，则该同学测得的折射率与真实值相比______（填“偏大”、“偏小”或“不变”）．

参考答案：（1）图中P1P2作为入射光线，OO′是折射光线，设光线在玻璃砖上表面的入射角为i，折射角为r，则由几何知识得到：sini=ABAO，sinr=CDOC，又AO=OC，则折射率n=sinisinγ=ABCD=1.5．
（2）如图，实线是真实的光路图，虚线是玻璃砖宽度画大后的光路图，由图看出，在这种情况测得的入射角不受影响，但测得的折射角比真实的折射角偏大，因此测得的折射率偏小．



故答案为：（1）1.5；（2）偏小．

本题解析：

本题难度：一般

3、实验题  学校开展研究性学习，某研究小组的同学根据所学的光学知识，设计了一个测量液体折射率的仪器，如图所示．在一圆盘上，过其圆心O作两条互相垂直的直径BC 、EF，在半径OA上，垂直盘面插下两枚大头针P1、P2，并保持P1、P2位置不变，∠AOF=30°，每次测量时让圆盘的下半部分竖直进入液体中，而且总使得液面与直径BC相平，EF作为界面的法线，而后在图中右上方区域观察P1、P2的像，并在圆周上插上大头针P3，使P3正好挡住P1、P2的像，同学们通过计算，预先在圆周EC部分刻好了折射率的值，这样只要根据P3所插的位置，就可直接读出液体折射率的值，则：

（1）若OP3与OC的夹角为30°，则P3处所对应的折射率的值为_________．
（2）图中P3、P4两位置哪一处所对应的折射率的值大？ ____________．
（3）若某种液体的折射率为n=2.5，可以用此仪器进行测量吗？_________．

参考答案：（1）
（2）P4（P4对应的折射率大）
（3）不可以（不能、不行）

本题解析：

本题难度：一般

4、填空题  如图所示，截面为等腰三角形的玻璃砖，顶角为30°，入射光线DO垂直于AB边射入玻璃内，从AC边射出时偏向角为30°，则此玻璃的折射率为______．

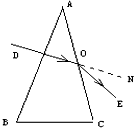
参考答案：当光垂直入射时，由于入射角为零，所以折射角也为零．
由于三棱镜的顶角是30°可知，当光再次入射时，入射角为30°，而折射角则为60°，
由折射定律可求出折射率n=sin60°sin30°=

本题解析：

本题难度：一般

5、计算题  如图所示，△ABC为一直角三棱镜的截面，其顶角θ=30°，P为垂直于直线BCD的光屏，现一宽度等于AB的单色平行光束垂直射向AB面，在屏P上形成一条宽度等于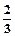的光带，试作出光路图并求棱镜的折射率。

参考答案：平行光束经棱镜折射后的出射光束仍是平行光束，如下图所示．图中θ1、θ2为AC面上入射角和折射角，根据折射定律，有

nsinθ1=sinθ2，
设出射光线与水平方向成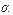角，则
θ2=θ1＋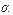
由于==?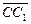
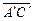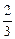
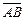所以=?
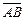而==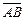tanθ
所以tan==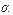
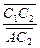可得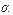=30°，θ2=60°，所以n==．

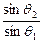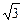本题解析：略

本题难度：一般