1、计算题 如图所示,总质量为460kg的热气球,从地面刚开始竖直上升时的加速度为0.5m/s2,当热气球上升到175m时,以10m/s的速度向上匀速运动,同时有一颗质量为0.01kg的小铆钉从热气球上脱离掉落,小铆钉脱离时相对热气球静止。若离开地面后热气球所受浮力保持不变,上升过程中热气球总质量不变,重力加速度g=10m/s2。求:

(1)热气球所受浮力大小;
(2)匀速上升时热气球所受的空气阻力;
(3)小铆钉落地时热气球离地的高度。
参考答案:(1)4 830 N;(2)230 N;(3)245m
本题解析:(1)气球匀加速上升过程中,受到向上的浮力,向下的重力,根据牛顿第二定律可得: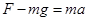 ,所以
,所以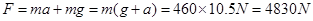
(2)匀速上升时,气球受到向下的重力,向上的浮力,和向下的阻力作用,三力合力为零,故有
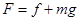 ,所以
,所以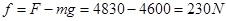
(3)小铆钉先做初速度为10m/s的竖直上抛运动,然后做自由落体运动,
竖直上抛运动时间为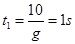 ,上升的高度为
,上升的高度为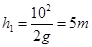
故小铆钉做自由落体运动的高度为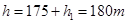
做自由落体运动时间为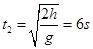
故气球上升的高度为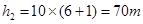
故此时气球离地的高度为:
考点:考查了牛顿第二定律,运动学公式的应用
本题难度:一般
2、计算题 如图所示,质量m=1kg的小物块放在一质量为M=4kg的足够长的木板右端,物块与木板间的摩擦因数μ=0.2,木板与水平面间的摩擦不计。物块用劲度系数k=25N/m的弹簧拴住,弹簧的另一端固定(与木板不粘连)。开始时整个装置静止,弹簧处于原长状态。现对木板施以F=12N的水平向右恒力,(最大静摩擦力可认为等滑动摩擦力,g=10m/s2)。已知弹簧的弹性势能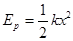 ,式中x为弹簧的伸长量或压缩量。求:
,式中x为弹簧的伸长量或压缩量。求:
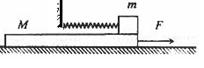
(1)开始施力的瞬间物块与木板的加速度各多大;
(2)物块达到的最大速度。
参考答案:(1)物块的加速度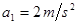 ,木板的加速度
,木板的加速度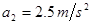 ;(2)
;(2)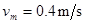 。
。
本题解析:开始施力的瞬间,弹簧还没有形变,不存在弹簧的弹力,分析物块与木板会不会有相同的加速度,是本题的关键。
(1)若物块与木板有相同的加速度,对整体受力分析,由牛顿第二定律,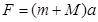 ,
,
解得: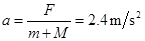
对物块受力分析,最大加速度: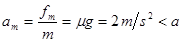 ,即开始施力后物块与木板即发生相对滑动。
,即开始施力后物块与木板即发生相对滑动。
刚施力时,弹簧不发生形变,根据牛顿第二定律,
对滑块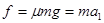 ,解得:
,解得: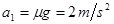
对木板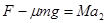 ,解得:
,解得: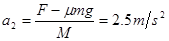
(2)随着物块不断向右运动,弹簧的形变量越来越大,对物块向左的弹力增大,物块做加速度不断减小的加速运动,当加速度减小到零时,速度增加到最大,即物块达到最大速度时所受合力为零。
有: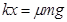
解得:
由动能定理: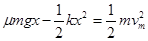
解得: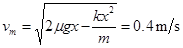
考点:牛顿第二定律的应用,摩擦力的特点,动能定理的应用。
本题难度:困难
3、计算题 如图所示,有一个水平匀强磁场,在垂直于磁场方向的竖直平面内放一个金属框,AB可以自由上下滑动,且始终保持水平,无摩擦。若AB质量为m=0.2g,长L=0.1m,电阻R=0.2Ω,其他电阻不计,磁感应强度B=0.1T,g=10m/s2。

(1)求AB下落速度为2m/s时,其下落的加速度及产生的热功率是多少?
(2)求AB边下落时的最大速度?
参考答案:(1)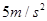 ,
, (2)
(2)
本题解析:(1)AB下落过程中切割磁感线产生的感应电动势为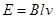 ,
,
受到的安培力为
通过AB的电流为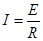
根据牛顿第二定律,AB运动的加速度为: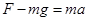
克服安培力做功,能量转化为电热,故热功率为
联立解得: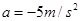 ,即加速度方向竖直向下,
,即加速度方向竖直向下,
(2)当重力和安培力相等时,AB的速度最大,即 ,解得
,解得
考点:考查了导体切割磁感线运动
本题难度:一般
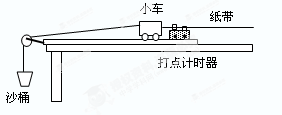
4、实验题 在“探究加速度与力、质量的关系”实验中,某同学使用了如图所示的装置.在实验过程中:
(1)为了探究加速度与质量的关系,应保持________不变(选填“m”、“ a”、“ F”);为了直观地判断加速度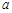 与质量
与质量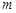 的数量关系,应作________图象(选填“
的数量关系,应作________图象(选填“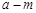 ”、“
”、“ ”) .
”) .
(2)该同学如图所示的实验操作中,还需要改进的地方有:
a
b
参考答案:(1) F; (2) 细绳子应 与水平面平行;应该平衡摩擦力
(2) 细绳子应 与水平面平行;应该平衡摩擦力
本题解析:
试题分析: 为了探究加速度与质量的关系,应保持合力F不变;根据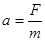 直观地判断加速度a与质量m的数量关系,应作
直观地判断加速度a与质量m的数量关系,应作 图象,因为是一条直线,更直观。
图象,因为是一条直线,更直观。
(2)要使小车前段的细线与长木板平行,使小车运动过程中所受的摩擦力不变;要适当使长木板的右端垫高,平衡摩擦力,保证小车的合外力等于沙桶的重力。
考点:探究加速度与力、质量的关系
本题难度:一般
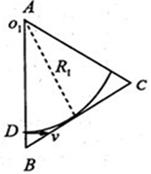
5、计算题 如图所示,M、N为中心开有小孔的平行板电容器的两极板,相距为D,其右侧有一边长为2a的正三角形区域,区域内有垂直纸面向里的匀强磁场,在极板M、N之间加上电压U后,M板电势高于N板电势.现有一带正电的粒子,质量为m,电荷量为q,其重力和初速度均忽略不计,粒子从极板M的中央小孔s1处射入电容器,穿过小孔s2后从距三角形A点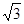 a的P处垂直AB方向进入磁场,试求:
a的P处垂直AB方向进入磁场,试求:

(1)粒子到达小孔s2时的速度和从小孔s1运动到s2所用的时间;
(2)若粒子从P点进入磁场后经时间t从AP间离开磁场,求粒子的运动半径和磁感应强度的大小;
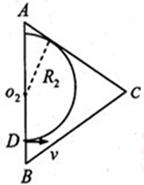
(3)若粒子能从AC间离开磁场,磁感应强度应满足什么条件?
参考答案:(1)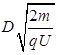 (2)
(2)  ,
,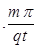 (3)
(3)
本题解析:(1)粒子在电场中运动时: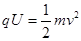
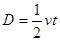 解得:
解得: ,
,
(2)粒子从进入磁场到从AD间离开: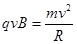
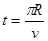 解得:
解得: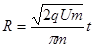 ,
,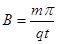
(3)粒子从进入磁场到从AC间离开,
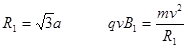 解得:
解得: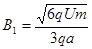
由图可知: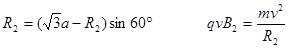
解得:
所以
考点:带电粒子在匀强电场中的加速;带电粒子在匀强磁场中的运动.
本题难度:困难