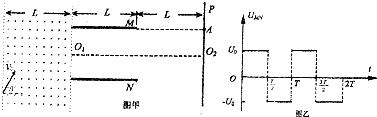
1、简答题  如图甲所示装置中，左侧是宽度为L的有界磁场，磁场方向垂直纸面向内．M、N为水平放置的平行导体板，长度为L，间距为d，加上电压后不考虑电场边缘效应，O1O2为两极板的中线．P是足够大的荧光屏，且屏与极板右边缘的距离也为L．质量为m、电荷量为e的电子从磁场左侧图示位置进入磁场，速度大小为v0，方向与水平成θ角．经过磁场偏转后，速度沿水平方向从O1位置进入MN板间区域，求：
（1）磁场磁感应强度B大小；
（2）若极板M、N间加恒定电压，电子经过电场偏转后正好打中屏上的A点，A点与极板M的同一水平线上，求M、N间所加电压U．
（3）若M、N间所加电压按如图乙所示周期性变化，要使电子磁场后在t=0时刻进入偏转电场后水平击中A点，试确定偏转电场电压U0以及周期T分别应该满足的条件．

参考答案：（1）电子经磁场偏转，洛伦兹力提供向心力，则有：evB=mveB；
由几何关系，L=Rsinθ?
解得：B=mv0sinθeL
（2）由题意知，电子经偏转电场偏转后做匀速直线运动到达A点，设电子离开偏转电场时的偏转角为θ，则由几何关系得：d2=（L+L2）tanθ?
解得：tanθ=d3L 又tanθ=vyv0?
vy=eUmdt
L=v0t
解得：U=md2v203eL2
（3）要使电子在水平在水平方向击中A点，电子必向上极板偏转，且vy=0，则电子应在t=0时刻进入偏转电场，且电子在偏转电场中运动的时间为整数个周期，设电子从加速电场射出的速度为v0，则
因为电子水平射出，则电子在偏转电场中的运动时间满足t=Lv0=nT?
则T=Lmv0 （n=1，2，3，4…）?
在竖直方向位移应满足 d2=2n×12 a（T2）2=2n×12?eU0md （T2）2?
解得：U0=2nmd2v20eL2 （n=1，2，3，4…）
答：（1）磁场磁感应强度B=mv0sinθeL．
（2）偏转电场所加电压为U=md2v203eL2．
（3）偏转电场电压为U0=2nmd2v20eL2 （n=1，2，3，4…），满足的周期关系为T=Lmv0 （n=1，2，3，4…）．

本题解析：

本题难度：一般

2、选择题  设想人类开发月球，不断把月球上的矿藏搬运到地球上，假定经过长时间开采后，地球仍可看作是均匀的球体，月球仍沿开采前的圆轨道运动，则与开采前相比（　　）
A．地球与月球间的万有引力将变大
B．地球与月球间的万有引力将不变
C．月球绕地球运动的周期将变长
D．月球绕地球的周期将变短

参考答案：A、B：设月球质量为m，地球质量为M，月球与地球之间的距离为r，
根据万有引力定律得：
地球与月球间的万有引力F=GMmr2，
由于不断把月球上的矿藏搬运到地球上，所以m减小，M增大．
由数学知识可知，当m与M相接近时，它们之间的万有引力较大，当它们的质量之差逐渐增大时，m与M的乘积将减小，它们之间的万有引力值将减小，故A、B错误．
C、D：假定经过长时间开采后，地球仍可看作是均匀的球体，月球仍沿开采前的圆周轨道运动（轨道半径r不变），
根据万有引力提供向心力得：GMmr2=m4π2T2r，T=2π

本题解析：

本题难度：一般

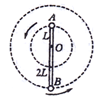
3、计算题  如图所示，轻杆长为3L，?在杆的A、B两端分别固定质量均为m的球A和球B，杆上距球A为L处的点O装在光滑水平转动轴上，杆和球在竖直面内转动，已知球A运动到最高点时，球A对杆恰好无作用力。求：
（1 ）球A在最高点时的角速度大小；
（2 ）球A在最高点时，杆对水平轴的作用力的大小和方向。

参考答案：解：（1）对A物体：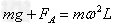

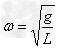
（2）对B物体：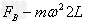

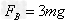
根据牛顿第三定律，球队杆向下的作用力为3mg，所以杆对水平轴的作用力大小3mg，方向竖直向下

本题解析：

本题难度：一般

4、选择题  如图所示，A、B两球质量相等，A球用不能伸长的轻绳系于O点，B球用轻弹簧系于O′点，O与O′点在同一水平面上，分别将A、B球拉到与悬点等高处，使绳和轻弹簧均处于水平，弹簧处于自然状态，将两球分别由静止开始释放，当两球达到各自悬点的正下方时，两球仍处在同一水平高度，则（　　）
A．两球到达各自悬点的正下方时，两球动能相等
B．两球到达各自悬点的正下方时，A球速度较大
C．两球到达各自悬点的正下方时，B球速度较大
D．两球到达各自悬点的正下方时，两球受到的拉力相等