1、选择题  如图所示的虚线区域内，充满垂直于纸面向里的匀强磁场和竖直向下的匀强电场。一带电粒子a（不计重力）以一定的初速度由左边界的O点射入磁场、电场区域，恰好沿直线由区域右边界的O′点（图中未标出）穿出。若撤去该区域内的磁场而保留电场不变，另一个同样的粒子b（不计重力）仍以相同初速度由O点射入，从区域右边界穿出，则粒子b

[? ]

参考答案：C

本题解析：

本题难度：一般

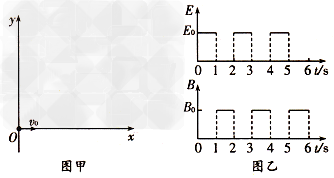
2、计算题  如图甲所示，在xoy平面内加有空间分布均匀、大小随时间周期性变化的电场和磁场，变化规律如图乙所示（规定竖直向上为电场强度的正方向，垂直纸面向里为磁感应强度的正方向）。在t=0时刻，质量m、电荷量为q的带正电粒子自坐标原点O处，以v0=2m/s的速度沿x轴正向水平射出。已知电场强度E0=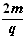、磁感应强度B0=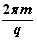，不计粒子重力。求：
（1）t=1s末粒子速度的大小和方向；
（2）1s—2s内，粒子在磁场中做圆周运动的半径和周期；
（3）画出0—4s内粒子的运动轨迹示意图（要求：体现粒子的运动特点）；
（4）（2n-1）s~2ns（n=1，2，3，……）内粒子运动至最高点的位置坐标。

参考答案：解：（1）在0~1s内，粒子在电场力作用下
带电粒子在x方向上做匀速运动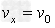
Y方向做匀加速运动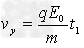
1s末粒子的速度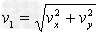
V1与水平方向的夹角α，则
代入数据解得，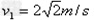
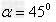
(2) 在1s~2s内，粒子在磁场中做圆周运动，由牛顿第二定律
?
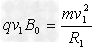得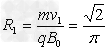m
粒子做圆周运动的周期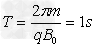
（3）粒子运动轨迹如图所示
?
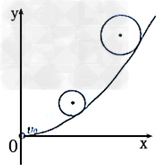（4）（2n-1）s末粒子的坐标为，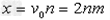
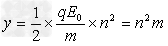
此时粒子的速度为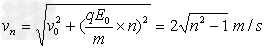
?
带电粒子在（2n-1）s~2ns（n=1，2，3…）内做圆周运动的轨迹如图所示

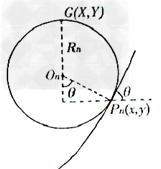
半径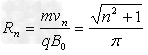m?
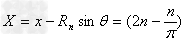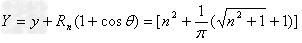最高点G的位置坐标为m m

本题解析：

本题难度：困难

3、计算题  (17分)如图所示，在xoy平面上，直线OM与x轴正方向夹角为45o，直线OM左侧存在平行y轴的匀强电场，方向沿y轴负方向。直线OM右侧存在垂直xoy平面向里的磁感应强度为B的匀强磁场。一带电量为q，质量为m带正电的粒子（忽略重力）从原点O沿x轴正方向以速度vo射入磁场。此后，粒子穿过磁场与电场的边界三次，恰好从电场中回到原点O。（粒子通过边界时，其运动不受边界的影响）

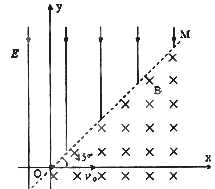
求： (1)粒子第一次在磁场中做圆周运动的半径；
(2)匀强电场的强度；
(3)粒子从O点射出至回到O点的时间。

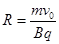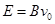参考答案：(1) ?(2) ?（3）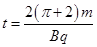

本题解析：（1）根据向心力公式可得：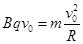
解得：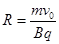
（2）粒子运动的轨迹如图所示：

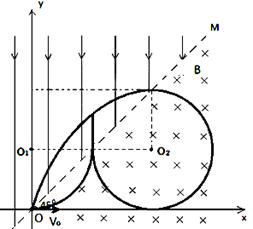
粒子第二次进入电场后做类平抛运动：
所以：；；
联立解得：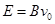
（3）粒子在磁场中运动的时间：

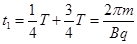
在电场中做直线运动的时间：

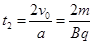
在电场中做类平抛运动的时间

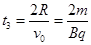
粒子从O点射出至回到O点的时间

本题难度：一般

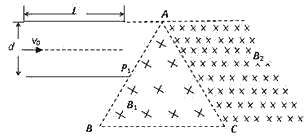
4、计算题  如图，左侧为两块长为L=10cm，间距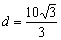cm的平行金属板，加上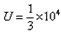V的电压，上板电势高；现从左端沿中心轴线方向入射一个重力不计的带电微粒，微粒质量m=10-10 kg，带电量q=+10-4 C，初速度v0=105m/s；中间用虚线框表示的正三角形内存在垂直纸面向里的匀强磁场B1，三角形的上顶点A与上金属板平齐，AB边的中点P1恰好在下金属板的右端点；三角形区域的右侧也存在垂直纸面向里，范围足够大的匀强磁场B2，且B2=4B1。求：
（1）带电微粒从电场中射出时的速度大小和方向；
（2）带电微粒进入中间三角形区域后，要垂直打在AC边上，则该区域的磁感应强度B1是多少？
（3）确定微粒最后射出磁场区域时的位置。

参考答案：解：（1）微粒在电场中做类平抛运动时间t，加速度a，射出电场时竖直方向的速度为vy
由牛顿第二定律有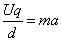
初速度方向匀速运动，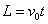
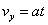
【或由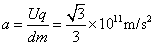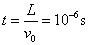，，得】
所以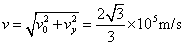
设v与水平方向夹角θ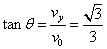，，所以垂直于AB出射
（2）带电粒子出电场时竖直方向偏转的位移y，有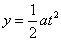，所以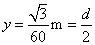，即粒子由P1点垂直AB射入磁场
设匀速圆周运动P1Q1段半径为R1，根据几何关系有：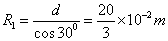
由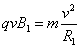得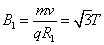
（3）带点粒子在B2磁场中以O2为圆心做匀速圆周运动，即Q1Q2段，其半径为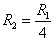
再次进入磁场B1区域时做以O3为圆心，半径仍为R1的匀速圆周运动，即Q2P2段，最后从P2点射出磁场区域。在△P2CO3中，根据数学知识，有CO3=0.5R1，线段P2C长度为：
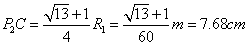（或距B端2.32cm）

本题解析：

本题难度：困难

5、填空题  如图所示，倾角为θ的光滑绝缘斜面，处在方向垂直斜面向上的匀强磁场和沿斜面方向的匀强电场中，有一质量为m、带电荷量为-q的小球，恰可在斜面上做匀速圆周运动、其角速度为ω，那么，匀强磁场的磁感应强度的大小为___________，未知电场的场强的大小为___________，方向沿___________。

参考答案：mω/q，mgsinθ/q，斜面向下

本题解析：

本题难度：一般