1、填空题  1992年7月，航天飞机“亚特兰蒂斯”号进行了一项卫星悬绳发电实验．航天飞机在赤道上空约300km处飞行，速度约为6.5×103m/s，方向由西向东，地磁场在该处的磁感应强度B=4×10-5T，地球半径为6400km，从航天飞机上释放了一颗卫星，卫星所携带的一根长L=20km的金属悬绳能产生的感应电动势约为______V．

参考答案：由切割磁感线产生的电动势得：
E=BLv=4×10-5×20×103×6.5×103V=5200?V

本题解析：

本题难度：简单

2、简答题  相距为L=0.20m的足够长的金属直角导轨如图所示放置，它们各有一边在同一水平面内，另一边垂直于水平面．质量均为m=1.0kg的金属细杆ab、cd与导轨垂直接触形成闭合回路，杆与导轨之间的动摩擦因数均为μ，导轨电阻不计，回路总电阻为R=1.0Ω．整个装置处于磁感应强度大小为B=0.50T，方向竖直向上的匀强磁场中．当ab杆在平行于水平导轨的拉力F作用下从静止开始沿导轨匀加速运动时，cd杆也同时从静止开始沿导轨向下运动．测得拉力F与时间t的关系如图所示．g=10m/s2，求：

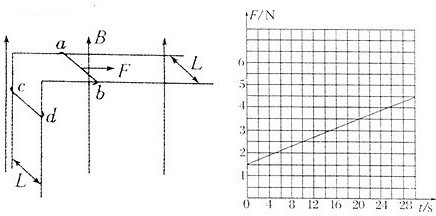
（1）杆ab的加速度a和动摩擦因数μ；
（2）杆cd从静止开始沿导轨向下运动达到最大速度所需的时间t0；
（3）画出杆cd在整个运动过程中的加速度随时间变化a-t图象，要求标明坐标值（不要求写出推导过程）．

参考答案：

（1）经时间t，杆ab的速率
? v=at
此时，回路中的感应电流为I=ER=BL?vR
对杆ab由牛顿第二定律得F-BIL-μmg=ma
由以上各式整理得：F=ma+μmg+B2L2Rat
在图线上取两点：
? t1=0，F1=1.5N；t2=30s，F2=4.5N，
代入上式得a=10m/s2，μ=0.5
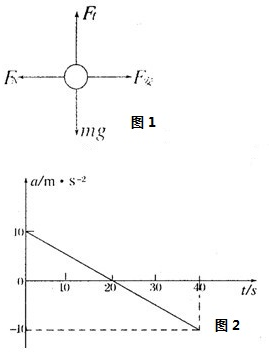
（2）cd杆受力情况如图1，当cd杆所受重力与滑动摩擦力相等时，速度最大，即mg=μFN．
又FN=F安?
? F安=BIL?
? I=ER=BL?vR
? v=at0
整理解得? t0=mgRμB2L2a=0.1×10×1.00.5×0.52×0.22×10s=20s
（3）设cd杆的加速度为a′，根据牛顿第二定律得：
mg-μF安=ma′
有：mg-μB2L2atR=ma′
得：a′=g-μB2L2atR，
当t=0时，a′=10m/s2；
当a′=0时，t=gRμB2L2=20s．故作出加速度随时间变化a-t图象如图2所示．
答：
（1）杆ab的加速度a和动摩擦因数μ分别为10m/s2和μ=0.5；
（2）杆cd从静止开始沿导轨向下运动达到最大速度所需的时间t0是20s．
（3）杆cd在整个运动过程中的加速度随时间变化a-t图象如图2所示．

本题解析：

本题难度：一般

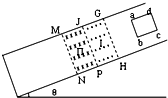
3、选择题  如图，在倾角为θ的光滑斜面上，存在着两个磁感应强度大小为B的匀强磁场，磁场的宽度MJ和JG均为L，一个质量为m、电阻为R、边长也为L的正方形导线框，由静止开始沿斜面下滑，当ab边刚越过GH进入磁场区时，恰好以速度?v1做匀速直线运动；当ab边下滑到JP与MN的中间位置时，线框又恰好以速度v2做匀速直线运动，从ab进入GH到MN与JP的中间位置的过程中，线框的机械能减少量为△E，重力对线框做功的绝对值为W1，安培力对线框做功的绝对值为W2，下列说法中正确的有（　　）
A．v2：v1=1：2
B．v2：v1=1：4
C．从ab进入GH到MN与JP的中间位置的过程中，W2等于△E
D．从ab进入GH到MN与JP的中间位置的过程中，线框动能变化量为W1-W2