1、计算题  如图所示，套在很长的绝缘直棒上的小球，其质量为m，带电荷量是+q，小球可在棒上滑动，将此棒竖直放在相互垂直且沿水平方向的匀强电场和匀强磁场中，电场强度为E，磁感应强度是B，小球与棒的动摩擦因数为μ，求小球由静止沿棒下落的最大加速度和最大速度．（设小球带电荷量不变）

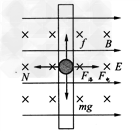
参考答案：解：小球的受力情况如题图所示
由于N=qE+qvB，所以F合=mg-μN= mg-μ(qE+qvB)
可见随着v的增大，F合减小，由牛顿第二定律可知，小球先做加速度越来越小的变加速运动，最后做匀速直线运动
故当v=0时，a最大，
当F合=0，即a=0时v有最大值vmax，即mg-μ(qvmaxB+qE) =0，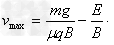

本题解析：

本题难度：一般

2、简答题  如图所示，在光滑绝缘的水平面上方，有一垂直纸面向里，磁感应强度为B的匀强磁场，水平面上，质量为m的不带电小球甲向右运动，与质量为2m，带电量为q的静止小球乙碰撞后连在一起运动，若碰撞后两球对水平面的总压力大小恰为mg，求碰前甲球的速度大小．

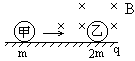
参考答案：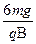

本题解析：

本题难度：一般

3、计算题  （19分）在图所示的坐标系中，x轴水平，y轴垂直，x轴上方空间只存在重力场，第Ⅲ象限存在沿y轴正方向的匀强电场和垂直xy平面向里的匀强磁场，在第Ⅳ象限由沿x轴负方向的匀强电场，场强大小与第Ⅲ象限存在的电场的场强大小相等。一质量为m，带电荷量大小为q的质点a，从y轴上y=h处的P1点以一定的水平速度沿x轴负方向抛出，它经过x= -2h处的P2点进入第Ⅲ ]象限，恰好做匀速圆周运动，又经过y轴上的y= -2h的P3点进入第Ⅳ 象限，试求：

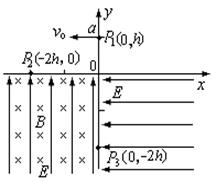
⑴质点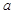到达P2点时速度的大小和方向；
⑵第Ⅲ象限中匀强电场的电场强度和匀强磁场的磁感应强度的大小；
⑶质点a进入第Ⅳ象限且速度减为零时的位置 坐标

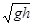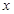参考答案：（1）v=2，其方向与轴负向夹角?θ=45°（2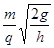）（3）

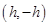
本题解析：（19分）如图所示。

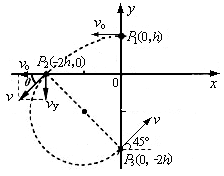
（1）质点在第Ⅱ象限中做平抛运动，设初速度为v0，由
……①?（2分）
2h=v0t…… ②?（2分）
解得平抛的初速度?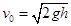?（1分）
在P2点，速度v的竖直分量（1分）
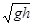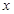所以，v=2，其方向与轴负向夹角?θ=45°?（1分）
（2）带电粒子进入第Ⅲ象限做匀速圆周运动，必有
mg=qE……③?（2分）
又恰能过负y轴2h处，故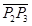为圆的直径，转动半径
R=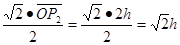?…… ④（1分）
又由?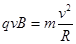……⑤ （1分）．　　
可解得　E ="mg/q" （1分）；
B = 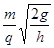（2分）
（3）带电粒以大小为v，方向与x轴正向夹45°角进入第Ⅳ象限，所受电场力与重力的合力为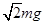，方向与过P3点的速度方向相反，故带电粒做匀减速直线运动，设其加速度大小为a，则：
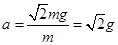……?⑥（2分）；?
由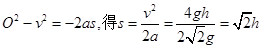（2分）
由此得出速度减为0时的位置坐标是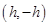（1分）

本题难度：一般

4、选择题  一个带电粒子在匀强磁场B中所受的洛仑兹力F的方向如图所示，则该粒子所带电性和运动方向可能是

[? ]
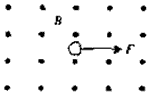
A．粒子带负电，向下运动
B．粒子带正电，向左运动
C．粒子带负电，向上运动
D．粒子带正电，向右运动

参考答案：A

本题解析：

本题难度：简单

5、计算题  （8分）如图所示为一速度选择器，板间存在方向互相垂直的匀强电场和磁场。现有速率不同的电子从A点沿直线AB射入板间。平行板间的电压为300 V，间距为5 cm，垂直纸面的匀强磁场的磁感应强度为0.06 T，问：

(1)匀强磁场的方向指向纸面里还是向外？
(2)能沿直线通过该速度选择器的电子的速率？

参考答案：(1) 垂直于纸面向里(2) 105m/s

本题解析：(1)由于电子所受到的电场力向上，由平衡知，洛伦兹力向下，由左手定则判断出 B的方向垂直于纸面向里（2分）
(2)电子受到的洛伦兹力为：FB=evB，它的大小与电子速率v有关，只有那些速率的大小刚好使得洛伦兹力与电场力相平衡的电子，才可沿直线KA通过小孔S
据题意，能够通过小孔的电子，其速率满足下式：evB=eE(2分)
解得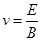：（1分）
又因为（2分）
所以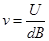得v=105m/s（1分）

本题难度：一般