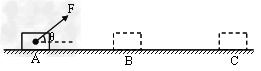
1、计算题  如图所示，一个质量为m=2.0kg的滑块静止放在水平地面上的A点，受到一个大小为10N，与水平方向成θ=37°角的斜向上恒力F作用开始运动，当物体前进L=1.0m到达B点时撤去F，滑块最终停在水平地面上的C点，滑块与地面间的滑动摩擦因数μ=0.2，求BC间的距离x。（cos37°=0.8，sin37°=0.6，g取10m/s2）

参考答案：解：对滑块从A到C由动能定理得：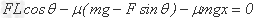
解得：x=1.3m

本题解析：

本题难度：一般

2、计算题  质量为5t的汽车从静止出发，以1m/s2的加速度沿平直公路行驶，已知汽车所受阻力为1000N，求：
（1）汽车的牵引力为多大？
（2）汽车在10s末的功率是多大？
（3）合外力在这段时间内对汽车做的功是多少？

参考答案：解：（1）由F－f=ma得，F=ma+f=6000N
（2）P=Fv=Fat=12kw
（3）W合=mv2/2=10000J

本题解析：

本题难度：一般

3、简答题  质量为M=4.0kg的平板小车静止在光滑的水平面上，如图所示，当t=0时，两个质量分别为mA=2kg、mB=1kg的小物体A、B都以大小为v0=7m/s．方向相反的水平速度，同时从小车板面上的左右两端相向滑动．直到它们在小车上停止滑动时都没有相碰，A、B与小车板面间的动摩擦因数均为μ=0.2，取g=10m/s2，求：
（1）A、B在车上都停止滑动时整体共同的速度
（2）A、B在小车上滑动过程中，系统损失的机械能
（3）从A、B开始滑动到都停止滑动一共经历了多长时间．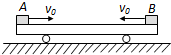

参考答案：（1）全过程，对系统，由动量守恒，令向右为正：
mAv0-mBv0=（M+mA+mB）v′
整体共同的速度为v′=1m/s?
（2）全过程，对系统，由能量守恒得
△E机=12mAv20+12mBv20-12（M+mA+mB）v′2
所以，系统损失的机械能：
△E机=70J?
（3）根据动量定理得：
F合t=△p=m△v
对滑块从开始滑动到相对小车停止滑动的过程有：
mgμ△t=m△v
所以滑块在小车上的滑动时间：△t=△vgμ
由于B滑块的速度变化△v比A滑块大，所以相对小车的滑行时间长?
所以一共经历的滑行时间为：△t=△tB=△vBgμ=4s
答：（1）A、B在车上都停止滑动时整体共同的速度是1m/s?
（2）A、B在小车上滑动过程中，系统损失的机械能是70J?
（3）从A、B开始滑动到都停止滑动一共经历了4s．

本题解析：

本题难度：一般

4、计算题  某幼儿园的滑梯如图所示，其中AB段为一倾角为的粗糙斜面，BC段为一段半径为R的光滑圆弧，其底端切线沿水平方向.若一儿童自A点由静止滑到C点时，对C点的压力大小为其体重的n倍，已知A与B、B与C间的高度差分别为h1、h2，重力加速度为g，求：

（1）儿童经过B点时的速度大小；
（2）儿童与斜面间的动摩擦因数.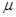

参考答案：（1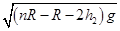）?（2）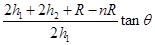

本题解析：（1）儿童对C处的压力大小为F，由牛顿第二定律可知：
?
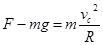儿童由B至C，由机械能守恒可知：?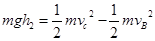
由以上两式可得：?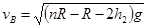
（2）设儿童与斜面 间的动摩擦因数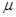，儿童所受摩擦力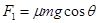
儿童由A至B，由动能定理可知：?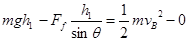
综上可得：?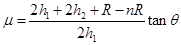
点评：本题是动能定理和机械能守恒的基础应用，在机械能不守恒时，如果涉及能量一般使用动能定理。

本题难度：一般

5、简答题  物体在斜坡上A处由静止开始滑下，如图所示．滑到B处后又沿水平直路前进到C处停下．如果物体在A处以一定的初速度v0=10m/s滑下，求物体停下处D距C多远？斜坡AB与直路BC用一段极短的圆弧连接，物体可视为质点且与路面的摩擦系数处处相同为μ=0.5．（g=10m/s2）

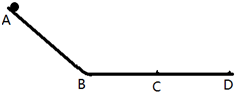
参考答案：设斜坡的倾角为α，高度为h，斜坡长为s，物体从在斜坡上A处由静止开始滑下直到C处停止的过程，应用动能定理得
mgh-μmgcosα?s-μmgsBC=0 ①
再对物体在A处以一定的初速度v0=10m/s滑下的全过程，运用动能定理得
mgh-μmgcosα?s-μmg（sBC+sCD）=0-12mv20 ②
由②-①式可得 sCD=v202μg
代入数据得：物体停下处D距C点距离为sCD=10m
答：物体停下处D距C点距离为10m．

本题解析：

本题难度：一般