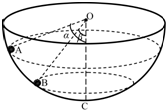
参考答案：A、根据平行四边形定则得，N=mgcosθ，则NANB=cos37°cos53°=43．故A正确．
B、根据mgtanθ=mv2r=mr(2πT)2，r=Rsinθ，解得v=

本题解析：

本题难度：一般

2、简答题  （1）如图所示，线圈abcd的面积是0.05m2，共100匝；线圈总电阻r=1Ω，外接电阻R=9Ω，匀强磁场的磁感应强度B=

参考答案：（1）①感应电动势最大值为Em=NBSω=100×1π×0.05×100V=500V
由于从中性面开始计时，则瞬时值表达式为：e=Emsin（ωt）=500sin（100πt）V
②流过电阻R的最大电流Im=EmR+r=5009+1A=50A
通过电阻R的电流有效值I=

本题解析：

本题难度：一般

3、简答题  一质量m=2kg的小球从光滑斜面上高h=3.5m处由静止滑下，斜面底端紧接着一个半径R=1m的光滑圆环，如图所示，试求：（g=10m/s2）
（1）小球滑至圆环顶点时对环的压力；
（2）小球至少应从多高处由静止滑下才能越过圆环最高点；
（3）小球从h"=2m处由静止滑下时，脱离圆环的位置和圆心的连线与竖直方向夹角的余弦．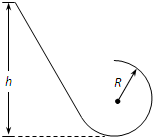

参考答案：（1）设小球滑至环顶时的速度为υ1，所受环的压力为N．
小球运动过程中机械能守恒：mg(h-2R)=12mυ21①
在顶点由圆周运动的知识有：mg+N=mυ21R②
联立①②解得：N=mg(2hR-5)（
代入数值解得：N?=2×10(2×3.51-5)N=40N
由牛顿第三定律知小球对环的压力大小为：N"=N=40N
（2）当圆环对小球的压力为零时，仅由重力充当向心力，对应的速度υ2为越过圆环最高点的最小速度，对应的高度h1为最低高度，由机械能守恒定律及圆周运动知识有：mg(h1-2R)=12mυ22③
mg=mυ22R④
联立③④解得：h1=52R=2.5m
（3）由于h"＜h1，故球在还没有到达顶端前即与环脱离，设脱离圆环时的位置半径与竖直方向的夹角为α，选轨道最低点为零势点，由机械能守恒定律及圆周运动知识有：mgh′=12mυ2+mgR(1+cosα)⑤
mgcosα=mυ2R⑥
联立⑤⑥解得：cosα=2(h′-R)3R=23
答：（1）小球滑至圆环顶点时对环的压力为40N．
（2）小球至少应从2.5m高处由静止滑下才能越过圆环最高点．
（3）小球从h"=2m处由静止滑下时，脱离圆环的位置和圆心的连线与竖直方向夹角的余弦为23．

本题解析：

本题难度：一般

4、简答题  如图，在平面直角坐标系xOy内，第Ⅰ象限存在沿y轴负方向的匀强电场，第Ⅳ象限以ON为直径的半圆形区域内，存在垂直于坐标平面向外的匀强磁场，磁感应强度为B．一质量为m、电荷量为q的带正电的粒子，从y轴正半轴上y=h处的M点，以速度v0垂直于y轴射入电场，经x轴上x=2h处的P点进入磁场，最后以垂直于y轴的方向射出磁场．不计粒子重力．求
（1）电场强度大小E；
（2）粒子在磁场中运动的轨道半径r；
（3）粒子从进入电场到离开磁场经历的总时间t．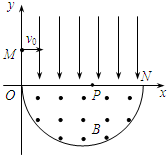

参考答案：

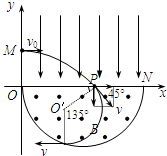
粒子的运动轨迹如右图所示
（1）设粒子在电场中运动的时间为t1
x方向匀速直线运动，则有：2h=v0t1
y方向初速度为零的匀加速直线运动，则有：h=12at12
根据牛顿第二定律：Eq=ma?
求出匀强电场强度：E=mv022qh
（2）粒子在电场中运动，根据动能定理：Eqh=12mv2-12mv02
设粒子进入磁场时速度为v，根据Bqv=mv2r
求出运动轨道的半径：r=

本题解析：

本题难度：一般

5、简答题  有一辆质量为800kg的小汽车驶上圆弧半径为40m的拱桥．（g取10m/s2）
（1）汽车到达桥顶时速度为5m/s，求汽车对桥的压力？
（2）汽车以多大速度经过桥顶时便恰好对桥没有压力？

参考答案：（1）汽车经过桥顶时，受力分析如图，重力和支持力的合力提供向心力，则：mg-N=mv2R
代入相关数据解得：N=7500N
由牛顿第三定律，汽车对桥的压力为：N′=N=7500N，方向竖直向下
（2）汽车对桥没有压力时，汽车只受重力，重力提供向心力，则有：mg=mv2R
解得：v=

本题解析：

本题难度：一般