1、选择题 水平台球桌面上母球A、目标球B和球袋洞口边缘C位于一条直线上,设A、B两球质量均为0.25kg且可视为质点,A、B间的距离为5cm,B、C间距离为x=160cm,因两球相距很近,为避免“推杆”犯规(球杆推着两球一起运动的现象),常采用“点杆”击球法(当球杆杆头接触母球的瞬间,迅速将杆抽回,母球在离杆后与目标球发生对心正碰,因碰撞时间极短,可视为完全弹性碰撞),设球与桌面的动摩擦因数为μ=0.5,为使目标球可能落入袋中,求:
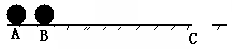
①碰撞过程中A球对B球的最小冲量为多大(碰撞过程中的摩擦阻力可忽略不计)
②碰撞前瞬间A球的速度最小是多大
参考答案:1kg·m/s? 4m/s
本题解析:①设碰撞后瞬间B球能进入球袋的最小速度为vB,由动能定理得:
μmgx=0-=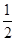 mvB2?解得vB="4m/s" (2分)
mvB2?解得vB="4m/s" (2分)
由动量定理得:I=mvB=1kg·m/s?(2分)
②设A碰撞前瞬间最小速度为vA,碰撞后瞬间为v,则:
由动量守恒定律得:mvA=mv+mvB?(2分)
由机械能守恒得: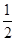 mvA2=
mvA2=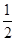 mv2+
mv2+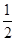 mvB2?(2分)
mvB2?(2分)
联立方程解得:vA=vB=4m/s,v=0?(1分)
本题难度:一般
2、简答题 一质子以1.0×107 m/s的速度与一个静止的未知核碰撞.已知质子的质量是1.67×10-27 kg,碰撞后质子以6.0×106 m/s的速度反向弹回,未知核以4.0×106 m/s的速度运动.试确定未知核的“身份”.
参考答案:氦核
本题解析:以质子和未知核组成的系统作为研究对象.它们碰撞时,系统的动量守恒.
设质子碰撞前的运动方向为正方向,则其碰撞前的速度v1=1.0×107 m/s,碰撞后的速度v1′=-6.0×106 m/s,质量m1=1.67×10-27 kg,设未知核的质量为碰后的速度m2,碰撞前的速度v2=0,碰撞后的速度v2′=4.0×106 m/s.
动量守恒定律m1v1+m2v2=m1v1′+m2v2′,有
m2=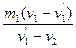 =
=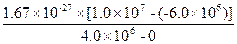 ?kg=6.68×10-27 kg
?kg=6.68×10-27 kg
对照元素周期表,可知该未知核是氦核.
本题难度:简单
3、选择题 质量为1kg的小球以4m/s的速度与质量为2kg的静止小球正碰,碰撞后的速度可能是
A.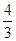 m/s,
m/s,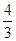 m/s
m/s
B.-1m/s,2.5m/s
C.1m/s,1.5m/s
D.-4m/s,4m/s
参考答案:ABC
本题解析:碰撞前后动量守恒,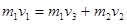 ,碰撞前的动能大于等于碰撞后的动能,
,碰撞前的动能大于等于碰撞后的动能, ,碰撞后小球1的速度反向或小于原来的速度
,碰撞后小球1的速度反向或小于原来的速度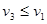 ,可得ABC可能
,可得ABC可能
本题难度:简单
4、选择题 如图所示,在光滑绝缘的水平直轨道上有两个带电小球a和b,a球质量为2m、带电量为+q,b球质量为m、带电量为+2q,两球相距较远且相向运动。某时刻a、b球的速度大小依次为v和1.5v,由于静电斥力的作用,它们不会相碰。则下列叙述正确的是(?)
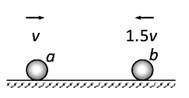
A.两球相距最近时,速度大小相等、方向相反
B.a球和b球所受的静电斥力对两球始终做负功
C.a球一直沿原方向运动,b球要反向运动
D.a、b两球都要反向运动,但b球先反向
参考答案:C
本题解析:本题利用动量守恒和功能关系求解比较简单,由于地面光滑,系统所受合外力为零,满足动量守恒条件,当两球速度相当等,系统损失机械能最大,两球相距最近.
水平方向系统动量守恒,由完全非弹性碰撞的知识可知,当两球速度相等时,系统损失机械能最大,两球相距最小,故A错误;
由题意可知,a球动量大于b球动量,因此系统动量水平向右,故b球运动过程中将反向运动而a球将一直沿原方向运动,(或者根据牛顿第二定律分析,此时a、b速度大小一样,而b的减速的加速度大,故b先减为零,然后反向加速运动),因此静电斥力对b球先做负功后做正功,故BD错误,C正确.
故选C.
点评:根据系统运动情况,选用正确规律求解是解题的关键,如在本题中,库仑力为内力,系统外力为零,因此动量守恒,利用动量守恒解答要简单很多.
本题难度:一般
5、选择题 如图所示是用频闪照相的方法拍摄到的一个弹簧振子的振动情况,甲图是振子静止在平衡位置时的照片,乙图是振子被拉到左侧距平衡位置20 cm处放手后向右运动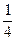 周期内的频闪照片,已知频闪的频率为10 Hz,则下列说法正确的是
周期内的频闪照片,已知频闪的频率为10 Hz,则下列说法正确的是
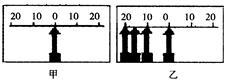
A.该振子振动的周期为1.6 s
B.该振子振动的周期为1.2 s
C.振子在该 1/4周期内做加速度逐渐减小的变加速运动
D.从图乙可以看出再经过0.2 s振子将运动到平衡位置右侧10 cm处
参考答案:BC
本题解析:略
本题难度:简单