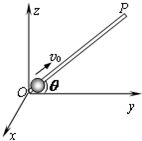
1、简答题  用两根绳子吊起一个重物，如图所示．如果AO和BO两根绳所能承受的最大拉力都是200N，求：（sin37°=0.6，sin53°=cos37°=0.8?）
（1）当重物重150N时，AO和BO绳中的张力（即产生的拉力）各是多大？
（2）该装置所能吊起的重物最重是多少牛？此时AO和BO绳中的张力又各是多大？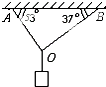

参考答案：（1）当重物重150N时，根据合成法知，TAO=Gsin53°=120N，TBO=Gcos53°=90N．
（2）假设两绳均不被拉断．分析O点受力情况，作出力图，如图．由图看出，TBO＜TAO，说明绳子AO的拉力先达到最大值，则知AO绳先断．


由上知，当AO绳的拉力达到最大时此时所吊起的重物最重，最大重力为G=TA0sin53°=2000.8N=250N．
此时TAO=200N，TBO=Gcos53°=150N．
答：（1）当重物重150N时，AO和BO绳中的张力（即产生的拉力）各是120N，90N．
（2）该装置所能吊起的重物最重是250N，此时AO和BO绳中的张力各是200N，150N．

本题解析：

本题难度：一般

2、填空题  如图所示，重为G的均匀棒水平地搁在一个圆柱体B上．二者的接触点D离棒的左端距离是棒长的3/5，当圆柱体顺时针方向转动时，在棒的右端与它紧靠着的木板C恰能沿光滑竖直墙面匀速下滑，则木板C的重为______．若木棒与圆柱体间的动摩擦因素为μ，则棒与圆柱体间的滑动摩擦力为______．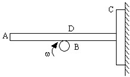

参考答案：因为棒均匀，令棒长为L，c对棒的摩擦力为f，则重力在L2处，以D为支点棒满足力矩平衡，有：
G?(35L-L2)=f?(L-35L)
可解得f=G4
以C为研究对象，因为C匀速下降，故C处于平衡状态，棒对C的摩擦力等于C的重力
根据牛顿第三定律可得：GC=f=G4
（2）以棒为研究对象，在竖直方向受重力、C对棒竖直向下的摩擦力f和B对D点竖直向上的弹力N作用，根据平衡可得：
G+f=N
所以N=G+f=5G4
所以棒与圆柱体间的滑动摩擦力f滑=μN=μ5G4
故答案为：G4，μ5G4

本题解析：

本题难度：一般

3、填空题  如图所示，物体在拉力的作用下，沿水平面向右做匀速直线运动，由此可知，物体所受的摩擦力与拉力的合力方向一定是______．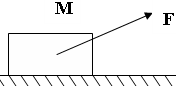

参考答案：

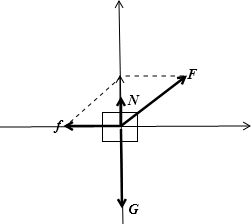
木块受到重力G、地面的支持力N和摩擦力f、拉力F的作用而做匀速直线运动，拉力方向斜向上，地面对物体的支持力小于重力，则重力与支持力的合力方向竖直向下，根据平衡条件推论可知，摩擦力与拉力的合力方向和重力与支持力的合力方向相反，而重力与支持力的合力方向竖直向下，则知摩擦力与拉力的合力方向竖直向上．
故答案为：竖直向上

本题解析：

本题难度：一般

4、计算题  在建筑装修中，工人用质量为5kg的磨石A对地面和斜壁进行打磨，已知磨石A与地面和斜壁之间的动摩擦因数μ均相同。
（1）当用水平方向的推力F1=25N推A打磨地面时，A恰好在水平地面上匀速运动，求A与地面间的动摩擦因数μ。
（2）若用A对与竖直方向夹角θ=37°为的斜壁进行打磨如图，当对A加竖直向上的推力F2=60N时，则磨石从静止开始沿斜壁向上运动2m（斜壁足够长）所需的时间为多少？（g取10m/s2，sin37°=0.6，cos37°=0.8）

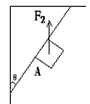
参考答案：解：（1）F1=μmg ①
μ=0.5
（2）(F2－mg)cosθ－μ(F2－mg)sinθ=ma ②
X=at2/2 ③
X=2m

本题解析：

本题难度：一般

5、选择题  在空间yOz平面内的光滑绝缘细杆OP与y轴正方向成θ角固定，杆上套有一带正电小球．使小球从O点以初速度v0沿杆上滑，某时刻起在杆所在空间加一电场或磁场，以下所加的“场”，能使小球在杆上匀速运动的是（　　）
A．沿z轴正方向的匀强电场
B．沿x轴负方向的匀强磁场
C．沿y轴负方向的匀强电场
D．沿x轴正方向的匀强磁场