1、选择题  如图，圆柱体的仓库内有三块长度不同的滑板aO、bO、cO，其下端都固定于底部圆心O，而上端则搁在仓库侧壁，三块滑块与水平面的夹角依次为300、450、600。若有三个小孩同时从a、b、c处开始下滑（忽略阻力），则（?）

A．a处小孩最先到O点
B．b处小孩最先到O点
C．c处小孩最先到O点
D．a、c处小孩同时到O点

参考答案：B

本题解析：三块滑块虽然都从同一圆柱面上下滑，但a、b、c三点不可能在同一竖直圆周上，所以下滑时间不一定相等。设圆柱底面半径为R，则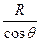=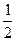gsinθt2，t2=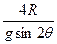，当θ=450时，t最小，当θ=300和600时，sin2θ的值相等。

本题难度：一般

2、简答题  卡车原来用7m/s的速度在平直公路上行驶，因为道口出现红灯，司机从较远的地方开始刹车，使卡车匀减速前进，当车速度减至1m/s时，交通灯转为绿灯，司机当即放开刹车，并且只用了原来一半的时间就加速到了原来的速度，从刹车开始到恢复原速过程用了9s，求：
（1）减速和加速过程中的加速度大小；
（2）开始刹车后2S末的瞬时速度大小．
（3）因过道口而耽误的时间．

参考答案：（1）卡车减速时，t1=23t=6s
a1=v1-v0t1=1-76m/s2=-1m/s2
即减速时加速度大小为1m/s2
卡车加速时，t2=13t=3s
a2=v2-v1t2=7-13m/s2=2m/s2
答：减速和加速的加速度大小分别为1m/s2、2m/s2．
（2）2秒末的速度v2
v2=v0+at=7+（-1）×2?m/s=5m/s
答：开始刹车后2S末的瞬时速度大小为5m/s．
（3）减速，加速的位移分别为S1、S2
S1=v0+v12t1=24m
S2=v1+v?2t2=12m
正常运行时间t0
t0=S1+S2vo=5.14s
耽误的时间△t△t=t-t0=3.86s
答：因过道口而耽误的时间为3.86s．

本题解析：

本题难度：一般

3、计算题  如图所示，绝缘传送带与水平地面成37°角，倾角也是37°的绝缘光滑斜面固定于水平地面上且与传送带良好对接，轻质绝缘弹簧下端固定在斜面底端。皮带传动装置两轮轴心相L="6" m，B、C分别是传送带与两轮的切点，轮缘与传送带之间不打滑。现将质量m=0.1kg、电荷量q="+2×" 10-5 C的工件(视为质点，电荷量保持不变)放在弹簧上，用力将弹簧压缩至A点后由静止释放，工件滑到传送带端点B时速度v0= 8m/s，AB间的距离s=1m，AB间无电场，工件与传送带间的动摩擦因数μ=0.25。（g取10m/s2。sin37°=0.6，cos37°=0.8）

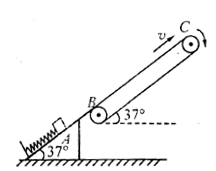
(1)求弹簧的最大弹性势能;
(2)若皮带传动装置以速度v顺时针匀速转动，且v可取不同的值(安全运行的最大速度为10 m/s)，在工件经过B点时，先加场强大小E=4×104 N/C，方向垂直于传送带向上的均强电场，0.5s后场强大小变为E"="1.2" ×105 N/C，方向变为垂直于传送带向下。工件要以最短时间到达C点，求v的取值范围;
(3)若用Q表示工件由B至C的过程中和传送带之间因摩擦而产生的热量，在满足(2)问的条件下，请推出Q与v的函数关系式。

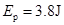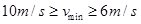参考答案：(1) ?(2) ?(3)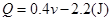

本题解析：(1) 从A到B的过程中，由机械能守恒定律有?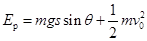
代入数据可得?，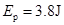
(2)工件经过B点运动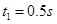?的过程中，根据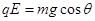?可知，摩擦力为零，工件做匀减速运动，故有：?，?，
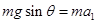所以?，?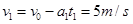
当场强大小变为?，方向变成垂直于传送带向下后，要使工件以最短时间到达C点，传送带对它的滑动摩擦力要一直向上，设满足此条件的传送带最小速度为?
根据牛顿第二定律有: ?，?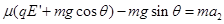
工件沿传送带发生的位移?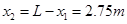
?，解得?
所以当传送带以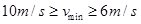?运动时，工件将以最短时间到达C点
(3) 由于第一个过程中摩擦力为零，所以只在第二个过程中产生热量，
在第二个过程中经历的时间为
传送带在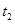时间内发生的位移
故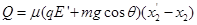
代入数据可得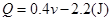

本题难度：一般

4、选择题  质点作直线运动的v-t图象如图所示，下列选项不正确的是（　　）
A．2s末物体的速度大小为4m/s
B．2～4s内物体做匀变速直线运动
C．3s末物体的速度为零，且改变运动方向
D．6s内物体做匀变速直线运动