1、选择题  带电离子a、b在同一匀强磁场中做匀速圆周运动，它们的动量大小相等，a运动的半径大于b运动的半径。若a、b的电荷量分别为qa、qb，质量分别为ma、mb，周期分别为Ta、Tb。则一定有
A．qa＜qb
B．ma＜mb
C．Ta＜Tb
D．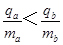

参考答案：A

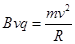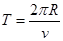本题解析：根据洛伦兹力提供向心力有，，可得离子的运动半径为，[学-科网离子的动量大小相等，且在同一个磁场中，则q与R成反比，已知Ra＞Rb，可得qa＜qb，A正确；已知它们的动量大小相等，但不知速度的大小关系，无法比较它们的质量大小关系，B错误；因为，不知速度的大小关系，无法比较它们的周期大小，C错误；因为不知道质量的关系，所以它们的比荷的大小关系不能确定，D错误。

本题难度：一般

2、选择题  一个所受重力可以忽略的带电粒子在磁感应强度为B的匀强磁场中做匀速圆周运动，如果它又垂直进入另一相邻的磁感应强度为2B的匀强磁场，则? (? )?
A．粒子的速率加倍，周期减半
B．粒子的速率不变，轨道半径减小
C．粒子的速率减半，轨道半径减为原来的1/4
D．粒子的速率不变，周期减半

参考答案：BD

本题解析：由于洛伦兹力永远不做功,所以粒子的速率不变，AC错；由半径公式可知半径变为原来的一半，由周期公式可知周期减半，BD正确
点评：难度较小，粒子在只受洛伦兹力的情况下做匀速圆周运动，由洛伦兹力提供向心力，洛伦兹始终不做功

本题难度：简单

3、填空题  如图11所示，一束电子（电量为e）以速度v垂直射入磁感强度为B，宽度为d的匀强磁场中，穿透磁场时速度方向与电子原来入射方向的夹角是30°，则电子的质量是?，穿透磁场的时间是?。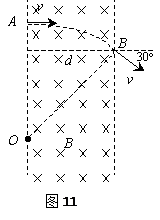

参考答案：m=2dBe/v?t=πd/3v。

本题解析：根据几何关系可知运动半径为2d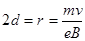，，所以可得电子质量m=2dBe/v
周期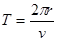，电子在磁场中转过30°角，所以穿透磁场的时间t=T/12=πd/3v
故答案为：m=2dBe/v? t=πd/3v

本题难度：简单

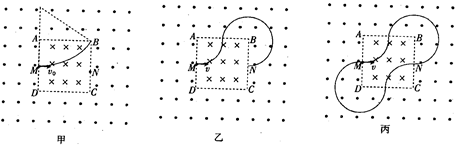
4、计算题  （18分）如图所示，竖直平面内边长为a的正方形ABCD是磁场的分界线，在正方形的四周及正方形区域内存在方向相反、磁感应强度的大小均为B的与竖直平面垂直的匀强磁场，M、N分别是边AD、BC的中点。现有一质量为m、电荷量为q的带正电粒子从M点沿MN方向射出，带电粒子的重力不计。

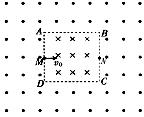
（1）若在正方形区域内加一与磁场方向垂直的匀强电场，恰能使以初速度v0射出的带电粒子沿MN直线运动到N点，求所加电场的电场强度的大小和方向。
（2）为使带电粒子从M点射出后，在正方形区域内运动到达B点，则初速度v0应满足什么条件?
（3）试求带电粒子从M点到达N点所用时间的最小值，并求出此条件下粒子第一次回到M点的时间。

参考答案：（1）E=Bv0方向竖直向下 ?（2）v0=5aqB/4m?（3）t’=2T=4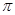m/qB

本题解析：（1）由题意，电场力与洛伦兹力平衡，有：qE=qv0B
解得E=Bv0
因带电粒子带正电，知电场强度的方向竖直向下
（2）此时，带电粒子的运动轨迹如图甲所示，
根据几何关系得R2=a2+(R-a/2)2
解得R=5a/4
由牛顿第二定律得qv0B=mv02/R
解得v0=5aqB/4m
（3）由题意可画出带电粒子的运动轨迹如图乙所示，可得带电粒子在两磁场中的轨道半径均为r=a/2
带电粒子在正方形区域内的运动时间t1=T/4
在正方形区域外的运动时间t2=3T/4
由qvB=4 m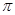2r/T2，可得T=2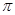m/qB
故带电粒子从M点到达N点所用时间的最小值t=t1+t2=2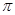m/qB ,
画出带电粒子从N点继续运动的轨迹如图丙所示，知带电粒子可以回到M点，由对称性，回到M点的时间为t’=2T=4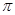m/qB

本题难度：一般

5、选择题  下列说法中正确的是（　　）
A．带电粒子在磁场中运动时，只有当其轨迹为圆时才有洛伦兹力不对带电粒子做功
B．不论带电粒子在磁场中做何运动，洛伦兹力均不对带电粒子做功
C．因为安培力是洛伦兹力的宏观表现，因而安培力使通电导体运动时，也不对导体做功
D．因为洛伦兹力对运动电荷不做功，因此带电粒子在磁场中运动时，它的速度不发生变化

参考答案：A、B、根据左手定则，洛伦兹力与速度垂直，永不做功，与运动情况无关，故A错误，B正确；
C、安培力是洛伦兹力的宏观表现，安培力可以做功，故C错误；
D、因为洛伦兹力对运动电荷不做功，因此带电粒子在磁场中运动时，它的速度大小不发生变化，但方向会改变，故D错误；
故选：B．

本题解析：

本题难度：简单