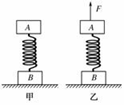
1、选择题  如图甲所示，水平面上质量相等的两木块A、B用一轻弹簧相连接，整个系统处于平衡状态.现用一竖直向上的力F拉动木块A，使木块A向上做匀加速直线运动，如图乙所示.研究从力F刚作用在木块A的瞬间到木块B刚离开地面的瞬间的这个过程，并且选定这个过程中木块A的起始位置为坐标原点，则下列图象中可以表示力F和木块A的位移x之间关系的是（ ?）

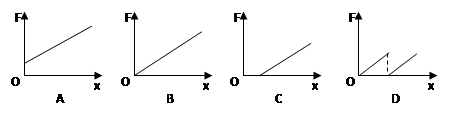
参考答案：A

本题解析：设弹簧的劲度系数为，A、B的质量为m，A的加速度大小为a,由题知整个系统处于平衡状态，此时弹簧的压缩量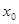满足：?①
当木块在平衡位置以下时，由牛顿第二定律可知：?②
由①②式得：F=kx+ma?③
当木块在平衡位置以上时，由牛顿第二定律可知：?④
由①④式得：F=kx+ma?⑤
由③⑤式可以看出力和木块的位移成一次函数关系，应选A

本题难度：一般

2、计算题  一根劲度系数为k、质量不计的轻弹簧，上端固定，下端系一质量为m的物体，有一水平板将物体托住，并使弹簧处于自然长度，如图所示。现让木板由静止开始以加速度a(a＜g)匀加速向下移动。求经过多长时间木板开始与物体分离。

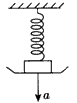
参考答案：解：设物体与平板一起向下运动的距离为x时，物体受重力mg、弹簧的弹力F=kx和平板的支持力N作用
据牛顿第二定律有：mg-kx-N=ma，得：N=mg-kx-ma
当N=0时，物体与平板分离，所以此时
因为，所以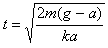

本题解析：

本题难度：一般

3、选择题  质量为2×103 kg的汽车，保持发动机输出功率为30×103 W不变，在水平公路上能达到的最大速度为15 m/s，当汽车的速度为10 m/s时，其加速度为多少？

参考答案：0.5 m/s2

本题解析：汽车速度最大时，受力平衡，即牵引力等于阻力，所以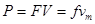，可求得阻力为2000N，当汽车的速度为10 m/s时，牵引力为3000N，根据牛顿第二定律可得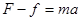，计算可知加速度为0.5 m/s2，
故答案为：0.5 m /s2

本题难度：简单

4、填空题  用6N水平拉力拉质量为2kg的物体，沿水平桌面匀速运动，若水平力改为10N，则物体的加速度大小为?m/s2。动摩擦因数为?（g=10m/s2）

参考答案：2? ,? 0.3

本题解析：物体做匀速直线运动时，有：．则．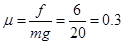
根据牛顿第二定律得，．
点评：根据物块做匀速直线运动，求出摩擦力的大小，从而求出物体与水平面的动摩擦因数．根据牛顿第二定律求出水平力为10N时的加速度．

本题难度：简单

5、计算题  如图所示，正面朝下的斜面与水平面夹角θ=37o，滑块质量m=1kg，滑块与斜面间的动摩擦因数μ=0.5，一个F=20N的水平推力作用在滑块上，滑块紧贴斜面加速下滑。试求：

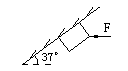
小题1:以质点表示滑块画出它的受力示意图；
小题2:求斜面对物块的弹力大小；
小题3:求物块所受的合力？（sin37o=0.6，cos37o=0.8，g=10N/kg）

参考答案：
小题1:

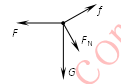
小题2:FN =4N
小题3:20N

本题解析：（1）如右图6所示，3分。出现多、漏、错力就不给分，可以不标字母。
（2）对物块，其受力正交分解如图所示 …………1分

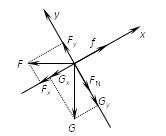
Fy合= Fy－FN－Gy =" 0" …………1分
即F·sinθ－FN－G·cosθ="0" …………2分
代入数据，解得FN ="4N" …………2分
（3）F合= Fx合= Fx + Gx－f…………1分
即 F合=F·cosθ+ G·sinθ－μFN…………2分
代入数据，解得F合="20N" …………1分
物块所受合力的方向沿斜面向下…………1分

本题难度：简单