1、简答题  有一半径为R的半圆形光滑绝缘槽，置于水平向右的匀强电场中，把一个带电量为+q的质量为m的小8球放在槽的B点使OB与竖直方向夹角θ=60°时刚好静止．若使小球从槽的边缘A点由静止释放，求：
（1）匀强电场的场强多大？
（2）小球运动到速度再次为零时，对应半径与竖直方向的夹角多大？此时绳子的拉力多大？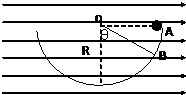

参考答案：（1）小球在B点处于平衡，有qE=mgtan60°．
解得E=

本题解析：

本题难度：一般

2、计算题  （20分）如图所示为一种获得高能粒子的装置。环形区域内存在垂直纸面向外、大小可调的匀强磁场。M、N为两块中心开有小孔的极板，每当带电粒子经过M、N板时，都会被加速，加速电压均为U；每当粒子飞离电场后，M、N板间的电势差立即变为零。粒子在电场中一次次被加速，动能不断增大，而绕行半径R不变（M、N两极板间的距离远小于R）。当t=0时，质量为m、电荷量为+q的粒子静止在M板小孔处。

（1）求粒子绕行n圈回到M板时的动能En；
（2）为使粒子始终保持在圆轨道上运动，磁场必须周期性递增，求粒子绕行第n圈时磁感应强度B的大小；
（3）求粒子绕行n圈所需总时间tn。

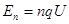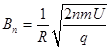参考答案：（1）?（2）（3）

本题解析：（1）粒子绕行一圈动能的增量为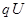，绕行n圈所获得的总动能（5分）
（2）因为 ?洛伦兹力提供向心力?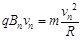
可得?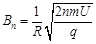?（6分）
（3）粒子做半径为R的匀速圆周运动，每一圈所用时间为，由于每一圈速度不同，所以每一圈所需时间也不同
第一圈： ?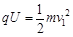
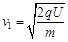
第二圈： ?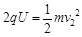
……
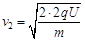
第n圈的速度?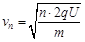?（4分）
故绕行n圈所需总时间
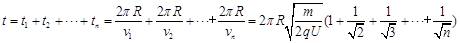?（5分）

本题难度：一般

3、简答题  如图所示，一长绝缘木板靠在光滑竖直墙面上，质量为m．木板右下方有一质量为2m、电荷量为+q的小滑块，滑块与木板间的动摩擦因数为μ，木板与滑块处在场强大小为E=4mg/q的匀强电场中，电场方向水平向左，若电动机通过一根绝缘细绳拉动滑块，使之匀加速向上移动，当滑块与木板分离时，滑块的速度大小为v．此过程中电动机对滑块做的功为W．（重力加速度为g）．
（1）求滑块向上移动的加速度大小；
（2）写出从滑块开始运动到与木板分离的过程中木板增加的机械能随时间变化的函数关系式．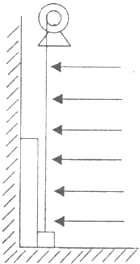

参考答案：（1）滑块与木板间的正压力大小为
FN=qE=4mg?
F=μFN?
对滑块W0一2mgh-Fh=12?2mv2?
v2=2ah?
由以上几式解得a=(1+2μ)mgv2W0-mv2?
（2）对长木板由牛顿第二定律得
F一mg=ma′
摩擦力对木板做功为W=Fx?
x=12a′t2
根据功能关系木板增加的机械能等于摩擦力所做的功，即△E=W
由以上各式解得△E=2（4μ一1）μmg2t2?
答：（1）滑块向上移动的加速度大小为(1+2μ)mgv2W0-mv2；
（2）从滑块开始运动到与木板分离的过程中木板增加的机械能随时间变化的函数关系式为△E=2（4μ一1）μmg2t2．

本题解析：

本题难度：一般

4、选择题  一子弹水平射入置于光滑水平面上的木块中，当子弹进入木块深2cm时，木块恰好移动1cm，在此过程，产生的热能与子弹损失的动能之比为（　　）
A．1：1
B．2：3
C．1：2
D．1：3

参考答案：产生的内能Q=f?X相? X相=2cm
根据动能定理得：-f?X=△Ek? X=3cm
所以产生的热能与子弹损失的动能之比为2：3，
故选B．

本题解析：

本题难度：一般

5、填空题  如右图所示，在长度一定的细线下方系一重量为G的小球，线的另一端固定，使悬线与竖直方向的夹角为θ=60°时无速释放小球.则小球摆回到最低点P时，细线所受力的大小是?.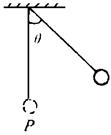

参考答案：2G

本题解析：由动能定理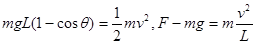,可求得拉力大小为2G
点评：本题难度较小，在最低点由绳子的拉力和重力的合力提供向心力

本题难度：一般