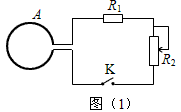
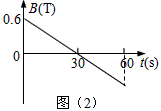
1、填空题  如图（1）所示，截面积S＝0.2m2，n＝100匝的圆形线圈A处在磁场中，磁场方向与线圈平面垂直，磁感应强度B随时间t变化的图象如图（2）所示，t＝0时刻，电键K闭合。已知R1＝4W，滑动变阻器R2的最大电阻为6W，线圈内阻不计，在滑动片移动的过程中，线圈A中的感应电流的最大值为___________A，滑动变阻器R2的最大功率为________________W。

参考答案：0.1；0.01

本题解析：

本题难度：一般

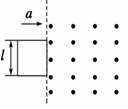
2、选择题  如图所示，虚线右侧存在匀强磁场，磁场方向垂直纸面向外，正方形金属框电阻为R，边长为l，自线框从左边界进入磁场时开始计时，在外力作用下由静止开始，以垂直于磁场边界的恒定加速度a进入磁场区域，t1时刻线框全部进入磁场．规定顺时针方向为感应电流I的正方向，外力大小为F，线框中电功率的瞬时值为P，通过线框横截面的电荷量为q，其中P－t图像为抛物线，则这些量随时间变化的关系正确的是

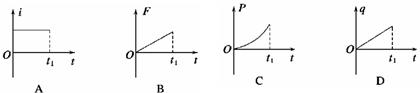
参考答案：C

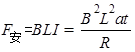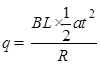本题解析：线框切割磁感线，则有运动速度v=at，产生感应电动势E=BLv，所以产生感应电流?，故A错误；对线框受力分析，由牛顿第二定律，则有?解得：，所以B错误；由功率表达式，，所以C正确；由电量表达式，则有?，所以D错误；
故选：C

本题难度：一般

3、选择题  如图所示，电阻为r的矩形线圈面积为S，在匀强磁场中绕垂直于磁场的轴以角速度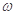匀速转动.t=0时刻线圈平面与磁场垂直，各电表均为理想交流电表.则：（?）

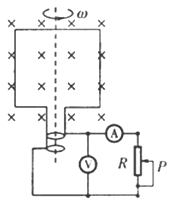
A．滑片P下滑时，电压表的读数不变
B．图示位置线圈中的感应电动势最大
C．线圈从图示位置转过1800的过程中，流过电阻R的电荷量为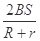
D．1s内流过R的电流方向改变次

参考答案：CD

本题解析：矩形线圈在匀强磁场中绕垂直于磁场的轴匀速转动时，线圈中产生正弦式交变电流，感应电动势最大值为Em=nBSω，线圈在磁场中匀速转动时产生的感应电动势最大值不变，有效值不变．滑片P下滑时，R增大，据闭合电路欧姆定律可知，通过R的电流有效值减小，线圈的内电压减小，则R的电压有效值增大，电压表的读数增大，故A错误；图示位置线圈中没有任何一边切割磁感线，线圈中感应电动势为零，由法拉第电磁感应定律可知磁通量的变化率为零，产生的电动势等于0；故B错误；线圈从图示位置转过180°的过程中，磁通量的大小相等，而方向相反，所以电路中的平均电动势大小：
平均电流：；流过电阻R的电量为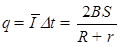：．故C正确；由题意得：线圈转动的周期为 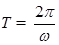，线圈每经过中性一次，感应电流方向改变一次，一周电流方向改变，所以1s内流过R的电流方向次数为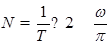：，故D正确．故选：CD．

本题难度：一般

4、简答题  面积S=0.2m2、n=100匝的圆形线圈，处在如图所示的磁场内，磁感应强度B随时间t变化的规律是B=0.02t，R=3Ω，C=30μF，线圈电阻r=1Ω，其余导线电阻不计，求：
（1）通过R的电流大小和方向．
（2）电容器C所带的电荷量．

参考答案：（1）由法拉第电磁感应定律可得：
E=n△?△t=n△BS△t=100×0.02×0.2V=0.4V；
则电路中电流I=ER+r=0.43+1=0.1A；
由题意知线圈中的磁通量增大，则由楞次定律可得线圈电流方向为逆时针，故R中电流方向从b指向a；
即通过R的电流大小为0.1A，方向从b指向a．
（2）由欧姆定律可得
R两端的电压U=IR=0.3V；
则电容器的电量Q=UC=9×10-6C；
即电容器的电荷量为9×10-6C．
答：（1）通过R的电流方向为b→a，
（2）电容器的电荷量为9×10-6C．

本题解析：

本题难度：一般

5、简答题  如图9-3-14所示，在磁感应强度为B的水平方向的匀强磁场中竖直放置两平行导轨，磁场方向与导轨所在平面垂直.导轨上端跨接一阻值为R的电阻（导轨电阻不计）.两金属棒a和b的电阻均为R，质量分别为ma=2×10-2 kg和mb=1×10-2 kg，它们与导轨相连，并可沿导轨无摩擦滑动.闭合开关S，先固定b，用一恒力F向上拉a，稳定后a以v1="10" m/s的速度匀速运动，此时再释放b，b恰好保持静止，设导轨足够长，取g="10" m/s2.

图9-3-14
（1）求拉力F的大小；
（2）若将金属棒a固定，让金属棒b自由滑下（开关仍闭合），求b滑行的最大速度v2.

参考答案：（1）0.4 N　（2）5 m/s

本题解析：（1）b棒静止，则有mbg=BIbL
b棒中的电流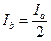
a棒匀速运动，则F=mag+BIaL
所以F=mag+2mbg="0.4" N.
（2）当a匀速运动时，产生的感应电动势Ea=BLv1
a棒中的电流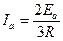
再由BIaL=2BIbL=2mbg
解得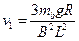
将a固定后，b达到最大速度，即匀速运动时

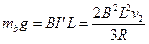
则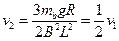
所以v2="5" m/s.

本题难度：简单