1、简答题  如图，一滑块通过长度不计的短绳拴在小车的板壁上，小车上表面光滑．小车由静止开始向右匀加速运动，经过2s，细绳断裂．细绳断裂后，小车的加速度不变，又经过一段时间，滑块从小车左端掉下，在这段时间内，已知滑块相对小车前3s内滑行了4.5m，后3s内滑行了10.5m．求
（1）小车底板长是多少？
（2）从小车开始运动到滑块离开车尾，滑块相对于地面移动的距离是多少？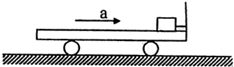

参考答案：设小车加速度为a．断裂时，车和物块的速度为v1=at=2a．断裂后，小车的速度v=v1+at，小车的位移
s1=v1t+12at2，滑块的位移s2=v1t
前3s，△s=s1-s2=12at2=4.5m，a=2△st2=1m/s2，v1=2m/s
设后3s初速度为v1′，则小车的位移s1′=v1′t+12at2，滑块的位移s2′=v1t
s1′-s2′=3v1′+4.5-3v1=10.5m，解得v1′=4m/s
由此说明后3s实际上是从绳断后2s开始的，滑块与小车相对运动的总时间为t总=5s．
（1）小车底板总长=s车-s滑=v1t总+12at2总-v1t总=12at2总=12.5m
（2）滑块在这段时间内的对地位移，s滑=v1t总=10m

本题解析：

本题难度：一般

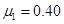2、计算题  如图所示，相距、质量均为M，两个完全相同木板A、B置于水平地面上，一质量为M、可视为质点的物块C置于木板A的左端。已知物块C与木板A、B之间的动摩擦因数均为，木板A、B与水平地面之间的动摩擦因数为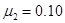，最大静摩擦力可以认为等于滑动摩擦力，开始时，三个物体均处于静止状态。现给物块C施加一个水平方向右的恒力F，且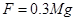，已知木板A、B碰撞后立即粘连在一起。

（1）通过计算说明A与B碰前A与C是一起向右做匀加速直线运动。
（2）求从物块C开始运动到木板A与B相碰所经历的时间。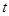
（3）已知木板A、B的长度均为，请通过分析计算后判断：物块C最终会不会从木板上掉下来？

参考答案：（1）见解析；（2）4s；（3）物块C将不会从木板上掉下来。   

本题解析：（1）设木板A与物块C之间的滑动摩擦力大小为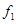，木板A与水平地面之间的滑动摩擦力大小为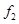，有：，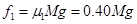
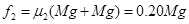
可见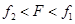，故可知在木板A、B相碰前，在F的作用下，木板A与物块C一起水平向右做匀加速直线运动。 （其他方法同样给分）  
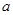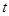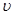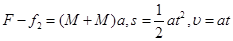（2）设此过程中它们的加速度为，运动时间为，与木板B相碰时的速度为，有：，解得：。    
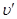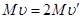（3）碰撞后瞬间，物块C的速度不变，设A、B碰后速度为，则得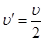
此即木板A、B共同运动的初速度。
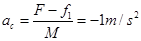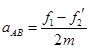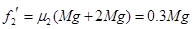此后，物块C在木板上滑动时的加速度为：，物块C在木板上滑动时，木板A、B共同运动的加速度为：，其中，解得：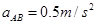
若木板A、B很长，则物块C不会掉下来。设物块C再运动时间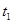后，三者的速度相同，有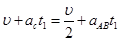：，解得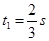：，在此过程中，物块C的位移为：
木板A、B的位移为：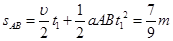
由于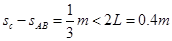，可见，物块C与木板A、B达到共同速度时还在木板上。进一步分析，由于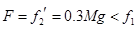，可知物块C将与木板A、B一起做匀速直线运动，可见物块C将不会从木板上掉下来。   
考点：动量及能量守恒定律；牛顿第二定律的综合应用.

本题难度：困难

3、填空题  一质点做匀变速直线运动，在第2s内的平均速度为6m/s，在第4s内的平均速度为10m/s．则该质点的加速度为______m/s2，第7s内位移为______m．

参考答案：匀加速直线运动平均速度等于中点时刻的速度，
所以v1.5=6m/s，v3.5=10m/s
所以a=△v△t=10-63.5-1.5=2m/s2，
第7s内位移为x=x7-x6=6×5.5+12×2×5.52-6×4.6-12×2×4.52=16m
故答案为：2?16

本题解析：

本题难度：一般

4、填空题  一辆汽车由静止开始做匀加速直线运动，加速8s后开始刹车，又经4s汽车才完全停下．设刹车过程中汽车做匀减速直线运动，那么前、后两段运动过程中，汽车位移的大小之比为______．

参考答案：汽车先匀加速后匀减速，设最大速度为v；
加速过程位移为：x1=0+v2?t1=4v
减速过程位移为：x2=v+02?t2=2v
故x1：x2=2：1；
故答案为2：1．

本题解析：

本题难度：简单

5、简答题  有一物体作直线运动，其速度图线如图所示．
（1）求出0-2s与4s-6s的加速度
（2）求出前6s内的位移？

参考答案：（1）0-2s的加速度a1=△v1△t13-02m/s2=1.5m/s2；
4s-6s的加速度a2=△v2△t2=-3-32m/s2=-3m/s2
（2）物体在0-5s内位移为x1=2+52×3m=10.5m
和5-6s内位移为x2=-3×12m=-1.5m
所以前6s内的位x=x1+x2=9m．
答：
（1）0-2s与4s-6s的加速度分别为1.5m/s2和-3m/s2．
（2）求出前6s内的位移为9m．

本题解析：

本题难度：一般