1、计算题  一铅球质量m=4 kg，从离沙坑面1.8m高处自由落下，铅球进入沙坑后下陷0.1 m静止，g=10m/s2，求沙对铅球的平均作用力．

参考答案：解：
方法一：铅球进入沙坑后不仅受阻力，还要受重力，从开始下落到最终静止，铅球受重力和沙的阻力的作用，重力一直做正功，沙的阻力做负功．
W总=mg(H +h)+(-F阻·h)，
铅球动能的变化△Ek= Ek末- Ek初=0．
由动能定理得△Ek=mg(H+h)+(-F阻·h)=0．
将H=1.8 m，h=0.1 m代入上式解得：
F阻=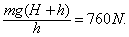
方法二：也可以分阶段分析做功：
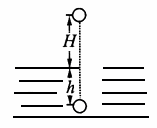
物体下落过程可分为两个过程(如图).
(1)自由落体下落H；
(2)在沙中减速下降h．这两个过程的联系是物体落至沙面时的速度即第一阶段的末速度为第二阶段的初速度．设这一速度为v，对第一段过程应用动能定理： ? ①
第二段过程物体受重力和阻力，同理可得： mgh-F阻h=0 -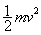? ②
由①②得F阻=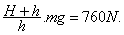

本题解析：

本题难度：困难

2、选择题  运动员投篮过程中对篮球做功为W，出手高度为h1，篮筐距地面高度为h2，球的质量为m，空气阻力不计，则篮球进筐时的动能为
A．mgh2－mgh1－W
B．W+mgh2－mgh1
C．mgh2+mgh1－W
D．W+mgh1－mgh2

参考答案：D

本题解析：篮球从由静止抛出到进入篮筐的过程中，人在对它做了功和它在上升过程中重力做了功，根据动能定理有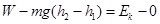，所以。
故选D
点评：容易题。本题要注意各个力做功的正负。

本题难度：简单

3、简答题  有一带负电的小球，其带电量q=-2×10-3C．如图所示，开始时静止在场强E=200N/C的匀强电场中的P点，靠近电场极板B有一挡板要S，小球与挡板S的距离h=5cm，与A板距离H=45cm，重力作用不计．在电场力作用下小球向左运动，与挡板S相碰后电量减少到碰前的k倍，已知k=

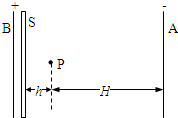
参考答案：
（1）S、P间电势差 U=US-UP，
又U=Eh=200×0.05=10V），
由题 US=0，则得UP=-10V
小球第一次到达挡板时，由动能定理得E=Eqh=200×2×10-3×5×10-2=0.02J
（2）根据动能定理得：W1=12mv2，W2=0-12mv2，
则小球从P点出发第一次回到最右端的过程中，电场力对小球做功 W=W1+W2=0
（3）由动能定理得? Eqh=12mv2，
当碰撞1次后，小球与挡板相碰后向右运动距离为h1，则 Ekqh1=12mv2，h1=1kh，
同理有 h2=1kh1…，
推得当碰撞n次后，hn=(1k)nh，
有h+H=(1k)nh，n=lgh+Hhlg1k=lg5+455lg65=12.5
所以小球经过13次碰撞后，才能抵达A板．
答：
（1）设匀强电场中挡板S所在位置处电势为零，则电场中P点的电势为-10V，小球第一次到达挡板S时的动能为0.02J；
（2）小球从P点出发第一次回到最右端的过程中，电场力对小球做功 W=W1+W2=0
（3）小球经过13次碰撞后，才能抵达A板．

本题解析：

本题难度：一般

4、简答题  如图所示：两块带电金属板a、b水平正对放置，在板间形成匀强电场，电场方向竖直向上．板间同时存在与电场正交的匀强磁场，假设电场、磁场只存在于两板间的空间区域．一束电子以一定的初速度v0从两板的左端中央，沿垂直于电场、磁场的方向射入场中，无偏转的通过场区．
已知：板长L=10.0cm，两板间距d=3.0cm，两板间电势差U=150V，v0=2.0×107m/s．电子所带电量与其质量之比e/m=1.76×1011C/kg，电子电荷量1.60×10-19C，不计电子所受的重力和电子之间的相互作用力．求：
（1）求磁感应强度B的大小
（2）若撤去磁场，求电子离开电场时偏离入射方向的距离y
（3）若撤去磁场，求电子穿过电场的整个过程中动能的增加量△EK（4）．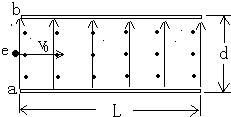

参考答案：
（1）由平衡条件得
? eUd=ev0B，得，B=Uv0d=2.5×10-4T
（2）若撤去磁场，电子做平抛运动．
水平方向：L=v0t
竖直方向：y=12at2，a=eUmd
联立得到，y=eUL22mdv20
代入解得，y=1.1×10-2m
（3）根据动能定理得
? 动能的增加量△EK=eEy=eUdy
代入解得，△EK=8.8×10-18J
答：
（1）磁感应强度B的大小为2.5×10-4T．
（2）若撤去磁场，求电子离开电场时偏离入射方向的距离y=1.1×10-2m．
（3）若撤去磁场，求电子穿过电场的整个过程中动能的增加量△EK=8.8×10-18J．

本题解析：

本题难度：一般

5、计算题  为了交通安全，在公路上行驶的汽车间应保持必要的距离，已知某高速公路的最高限速vm=120km/h，假设前方的车突然停车，后车驾驶员发现这一情况，经制动到汽车开始减速所通过的位移为17m，制动时汽车受到的阻力为汽车受到的重力的0.5倍，则高速公路上汽车间的距离至少应保持多远？（取g=10m/s2）

参考答案：解：制动时，路面的阻力对汽车做负功，汽车的动能减小
根据动能定理有- kmgs=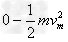
可得汽车制动后的滑行距离为s=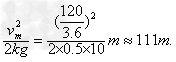
所求距离s总=s+s"= (117+17)m=128m

本题解析：

本题难度：一般