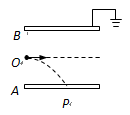
1、选择题  如图所示，在真空室中有一水平放置的不带电平行板电容器，板间距离为d，电容为C，上板B接地。现有大量质量均为m、带电量均为q的小油滴，以相同的初速度持续不断地从两板正中间沿图中虚线所示方向射入，第一滴油滴正好落到下板A的正中央P点。如果能落到A板的油滴仅有N滴，且第N+1滴油滴刚好能飞离电场，假定落到A板的油滴的电量能被板全部吸收，不考虑油滴间的相互作用，重力加速度为g，则下列说法正确的是(? )

A．落到A板的油滴数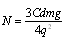
B．落到A板的油滴数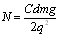
C．第N+1滴油滴通过电场的整个过程所增加的动能等于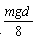
D．第N+1滴油滴通过电场的整个过程所减少的机械能等于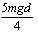

参考答案：A

本题解析：没有电荷时：?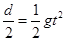
落到A板N滴油滴时：??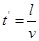
联立解得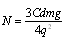：，A对。
第N+1滴油滴通过电场的整个过程，根据动能定理：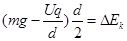


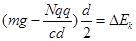
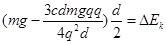
，C错；
减少的机械能等于克服电场力做的功。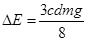，D错。

本题难度：一般

2、计算题  如图所示，ab、cd为一对水平正对放置的平行金属板，ab板在上、cd板在下，两板间距d＝0.10m，板长l＝2.0m，两板间电势差U＝1.0×104V。一带负电荷的油滴以初速度v0＝10m/s由两板中央沿垂直电场强度方向射入板间电场区，并能由bd端射出电场区。设电场区域仅限于两平行板之间，取g＝10m/s2
小题1:说明在带电油滴的比荷大小（q／m）不同时，油滴射入电场后可能发生的几种典型运动情况，指出运动性质。
小题2:求出上述几种典型运动情况中油滴的比荷大小（q／m）应满足的条件。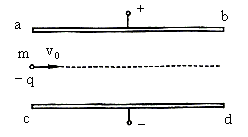

参考答案：
小题1:见解析
小题2:见解析

本题解析：

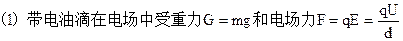
因为G和F均为恒力，所以有以下三种典型的运动情况：
?

?
（2）①在电场力大于重力的情况下，当油滴沿竖直方向的位移满足
?
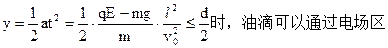因此在电场力大于重力的情况下油滴的比荷应满足
?
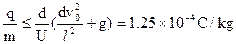②在电场力等于重力的情况下，应有qU/d＝mg??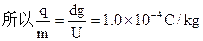
③在电场力小于重力的情况下，当油滴沿竖直方向的位移满足

因此在电场力小于重力的情况下油滴的比荷应满足
?

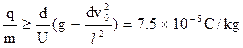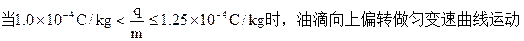
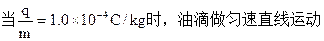
本题难度：一般

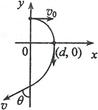
3、计算题  如图，在第一象限存在匀强磁场，磁感应强度方向垂直于纸面（xy平面）向外；在第四象限存在匀强电场，方向沿x轴负向。在y轴正半轴上某点以与x轴正向平行、大小为v0的速度发射出一带正电荷的粒子，该粒子在（d，0）点沿垂直于x轴的方向进人电场。不计重力。若该粒子离开电场时速度方向与y轴负方向的夹角为θ，求：

（1）电场强度大小与磁感应强度大小的比值；
（2）该粒子在电场中运动的时间。

参考答案：（1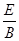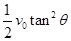）＝；（2）t＝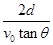

本题解析：（1）设磁感应强度的大小为B，粒子质量与所带电荷量分别为m和q，粒子进入磁场后做匀速圆周运动，并设其圆周运动的半径为r，根据牛顿第二定律和向心力公式有：qv0B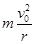＝? ①
由题设条件和图中几何关系可知：r＝d? ②
设电场强度大小为E，粒子进入电场后沿x轴负方向运动的速度大小为vx，由牛顿第二定律有：qE＝max? ③
根据运动学公式有：vx＝axt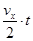，＝d? ④
由于粒子在电场中做类平抛运动（如图），有：tanθ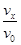＝? ⑤

由①②③④⑤式联立解得：＝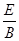
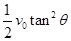
（2）由④⑤式联立解得：t＝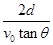

本题难度：一般

4、简答题  已知如图，匀强电场方向水平向右，场强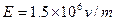，丝线长L=40cm，上端系于O点，下端系质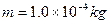量为，带电量为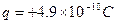的小球，将小球从最低点A由静止释放，求：

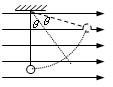
⑴小球摆到最高点时丝线与竖直方向的夹角多大？
⑵摆动过程中小球的最大速度是多大？

参考答案：74°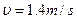　

本题解析：⑴这是个“歪摆”。由已知电场力Fe=0。75G摆动到平衡位置时丝线与竖直方向成37°角，因此最大摆角为74°。
⑵小球通过平衡位置时速度最大。由动能定理：?

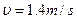
本题难度：简单

5、计算题  如图所示，一带电粒子电荷量为q=+2×10-10C,质量为m=1.0×10-12kg，从静止开始在电势差为U1的电场中加速后，从水平放置的电容器两极板正中央沿水平方向进入偏转电场，电容器的上极板带正电，电荷量为Q=6.0×10-9C，下极板接地，极板长10cm，两极板相距5cm，电容C=12pF（粒子重力不计）。求．：

（1）当U1=2000V时，粒子射出电容器的速率v和沿垂直于板面方向的偏移距离y；
（2）要使该粒子能从电容器中射出，加速电压U1的取值范围

参考答案：（1）1000m/s2;1.25cm（2）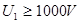

本题解析：离子经过加速电场的过程中，由动能定理得：
?
经过偏转电场的过程中，粒子仅受垂直于极板向下的静电力
平行板电容器的电压?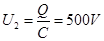
解法一：将粒子的运动分别沿v0方向（x）和垂直于v0方向（y）分解
x方向：
y方向：?
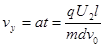
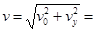1000m/s2?
?
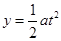
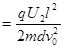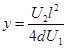=1.25cm?
解法二：由动能定理得
?

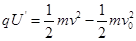联立得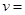1000m/s2?
要使电荷从电容器中射出，则必须满足条件
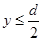?即??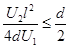
解得?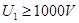
点评：本题难度中等，带电粒子在电场中做的是类平抛运动，计算电场力做功可利用公式W=qU计算，抓住临界条件是求解本题的关键

本题难度：一般