1、选择题 如图所示,粗糙程度均匀的绝缘斜面下方O点处有一正点电荷,带负电的小物体以某初速度从M点沿斜面上滑,到达N点时速度为零,然后下滑回到M点。若小物体电荷量保持不变,OM=ON,则:?(?)

A.小物体在上下滑动过程中经过同位置时受到摩擦力大小相等
B.小物体经过与O点距离最近处时受到的摩擦力最大
C.从M到N的过程中,摩擦力先增大后减小
D.小物体从M出发回到M的过程中,摩擦力做的功为零
参考答案:ABC
本题解析:略
本题难度:简单
2、简答题 关于“探究恒力做功与动能变化”的实验,下列说法中正确的是______.
A.应调节定滑轮的高度使细绳与木版平行
B.应调节定滑轮的高度使细绳保持水平
C.平衡摩擦力时,若纸带上打出的点越来越密,就应调大斜面倾角
D.平衡摩擦力时,若纸带上打出的点越来越疏,就应调大斜面倾角.
参考答案:A、应调节定滑轮的高度使细绳与木板平行,这样小车的合力可以认为就是绳的拉力.故A正确.
B、如果调节定滑轮的高度使细绳保持水平,而小车时放在倾斜的木板上,这样绳的拉力就不是小车的合力,实验就会产生较大的误差.
C、平衡摩擦力时,若纸带上打出的点越来越密,说明小车是减速下滑的,也就是小车的重力沿斜面分力小于摩擦力,那么我们应该调大斜面倾角,使得小车的重力沿斜面分力等于摩擦力.故C正确.
D、平衡摩擦力时,若纸带上打出的点越来越疏,说明小车是加速下滑的,也就是小车的重力沿斜面分力大于摩擦力,那么我们应该调小斜面倾角,使得小车的重力沿斜面分力等于摩擦力.故D错误.
故选AC.
本题解析:
本题难度:一般
3、计算题 如图所示,处于光滑水平面上的矩形线圈边长分别为L1和L2,电阻为R,处于磁感应强度为B的匀强磁场边缘,线圈与磁感线垂直。将线圈以向右的速度v匀速拉出磁场的过程。求:
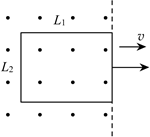
(1)拉力大小F;
(2)拉力的功率P;
(3)拉力做的功W;
(4)线圈中产生的电热Q;
(5)通过线圈某一截面的电荷量q。
参考答案:(1)F=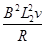 ;(2)P=
;(2)P=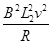 ;(3)W=
;(3)W= ;(4)Q=
;(4)Q= ;(5)q=
;(5)q=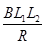
本题解析:
试题分析: (1)E=BL2v,I=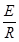 ,F=BIL2, ∴F=
,F=BIL2, ∴F=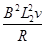 ?(2分)
?(2分)
(2)拉力的功率P=Fv=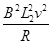 ?(2分)
?(2分)
(3)拉力做功W=FL1= ?(2分)
?(2分)
(4)根据功能关系Q=W=  ?(2分)
?(2分)
(5)通过导体横截面的电量q=I·t=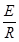 t=
t=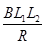 ?(2分)
?(2分)
本题难度:一般
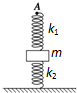
4、填空题 如图所示,劲度系数为k2的轻弹簧竖直放在桌面上(与桌面不粘连),上端固连一质量为m的物块.另一劲度系数为k1的轻弹簧下端固连在物块上.现将k1的上端A缓慢上提,当k2的弹力大小等于
mg时,m的重力势能增加了______,A点上升了______.
参考答案:对末态时的物块受力分析,受重力、弹簧K1的向上的拉力F1′与弹簧K2的向上的弹力F2′,物块静止有
F1′+F2′=mg
初态时,弹簧k2(压缩)的弹力F2=mg
末态时,弹簧k2(压缩)的弹力F2′=23mg
弹簧k2的长度变化量△x2=mg3k2
重力势能增加量△EP=mg△x2=(mg)23k2
由F1′+F2′=mg,F2′=23mg
得:F1′=13mg
初态时,弹簧k1(原长)的弹力F1=0
末态时,弹簧k1(伸长)的弹力F1′=13mg
弹簧k1的长度变化量△x1=△F1K1=mg3k1
由几何关系知所求距离为△x1+△x2=13mg(1k1+1k2)
故答案为:(mg)23k2,13mg(1k1+1k2)
本题解析:
本题难度:一般
5、计算题 (18分)把一个质量为m、带正电荷且电量为q的小物块m放在一个水平轨道的P点上,在轨道的O点有一面与轨道垂直的固定墙壁。轨道处于匀强电场中,电场强度的大小为E,其方向与轨道(ox轴)平行且方向向左。若把小物块m从静止状态开始释放,它能够沿着轨道滑动。已知小物块m与轨道之间的动摩擦因数μ,P点到墙壁的距离为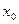 ,若m与墙壁发生碰撞时,其电荷q保持不变,而且碰撞为完全弹性碰撞(不损失机械能)。求:
,若m与墙壁发生碰撞时,其电荷q保持不变,而且碰撞为完全弹性碰撞(不损失机械能)。求:
(1)如果在P点把小物块 从静止状态开始释放,那么它第1次撞墙后瞬时速度为零的位置坐标 、第2次撞墙之后速度为零的位置坐标
、第2次撞墙之后速度为零的位置坐标 的表达式分别是什么?
的表达式分别是什么?
(2)如果在P点把小物块从静止状态开始释放,那么它最终会停留在什么位置?从开始到最后它一共走了多少路程(s)?
(3)如果在P点瞬间给小物块一个沿着x轴向右的初始冲量,其大小设为I,那么它第一次又回到P点时的速度(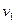 )大小为多少?它最终会停留在什么位置?从开始到最后它一共走了多少路程
)大小为多少?它最终会停留在什么位置?从开始到最后它一共走了多少路程 ?
?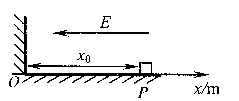
参考答案:(1) ;
;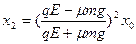
(2)它最终会停留在O点;
(3) ;小物块最终人会停留在O点;
;小物块最终人会停留在O点;
本题解析:
由题意分析知,小物块m沿着轨道滑动时,水平方向上受到二力:
滑动摩擦力 和电场力
和电场力
而且总是有: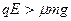 ?①
?①
(1)设第一次速度为零的位置坐标为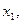 取墙面为零电势面,则在这一运动过程中应用功能关系有:
取墙面为零电势面,则在这一运动过程中应用功能关系有:
 ?②
?②
 ?③
?③
设第二次速度为零的位置坐标为
取墙面为零电势面,则在第二次运动过程中应用功能关系有:
 ?④
?④

即: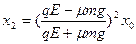 ?⑤
?⑤
(2)它最终会停留在O点。?⑥
对从开始到最终的整个运动过程应用功能关系有:
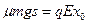 ?⑦
?⑦
 ?⑧
?⑧
(3)由动量定理知,小物块获得一个向右的初始冲量I,那么向右运动的初速度:
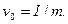 ?⑨
?⑨
设第一次瞬时速度为零的位置坐标为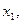
取墙面为零电势面,则在这一运动中应用功能关系有:
 ⑩
⑩
得: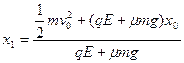 ?(11)
?(11)
即: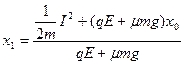 ?(12)
?(12)
同上道理,对从开始互第一次又回到P点这一过程应用功能关系有:
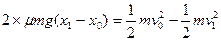 ?(13)
?(13)
得: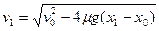
即: ?(14)
?(14)
小物块最终人会停留在O点。?(15)
设从开始到最后一共走的路程为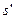 ,全过程应用功能关系有:
,全过程应用功能关系有:
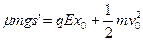 ?(16)
?(16)
得: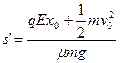
即: ?(17)
?(17)
本题难度:一般