1、选择题  某同学以校门口为原点，向东方向为正方向建立坐标，记录了甲、乙两位同学的位置—时间（x-t）图线，如图所示，下列说法中正确的是

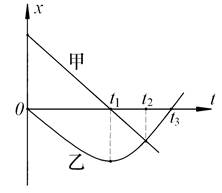
A．在t1时刻，甲的瞬时速度为零，乙的速度不为零
B．在t2时刻，甲、乙速度可能相同
C．在t2时刻，甲、乙两同学相遇
D．在t3时刻，乙的速度为零、加速度不为零

参考答案：C

本题解析：因为x-t图线的斜率等于物体的速度，所以在t1时刻，甲的瞬时速度不为零，乙的速度为零，选项A错误；在t2时刻，甲、乙速度方向不相同，所以速度不可能相同，选项B错误；在t2时刻，甲、乙两同学位移相同，所以两同学相遇，选项C正确；在t3时刻，乙的位移为零、速度不为零，加速度无法判断，选项D错误。

本题难度：一般

2、计算题  （14分）甲、乙两车在同一轨道上同向匀速行驶，甲车的速度为v1＝16m/s，乙车的速度为v2＝12m/s，乙车在甲车的前面，两车相距L＝6m。某时刻两车同时开始刹车，甲车的加速度为a1＝2m/s2，6秒后立即改做匀速运动，乙车刹车的加速度为a2＝1m/s2，求：
（1）从两车刹车到甲车第一次追上乙车的时间；
（2）两车相遇的次数。
（3）从两车刹车到两车速度相等经过的时间；

参考答案：（1） 2s?（2） 3次?（3） 4s? 8s

本题解析：（1）甲减速时，设经过t时间相遇，甲、乙位移分别为x1、x2，则：
?
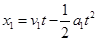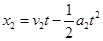
而x1=x2+L?解得：t1=2s，t2="6s" 则第一次甲追上乙用时2s
（2）当t2=6s时，甲车速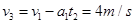?乙车速?则t2后乙车在前面，设再经过Δt甲追上乙，有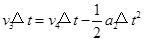?解得：Δt＝4s，此后，乙不能再追上甲，故甲乙相遇三次。
（3）设第一次等速经过的时间为t5，则?解得t5=4s。设第三次等速经过的时间为t6，则?解得：t6=8s

本题难度：一般

3、计算题  （12分）如图，甲、乙两运动员在训练接力赛的交接棒。已知甲、乙两运动员经短距离加速后都能达到并保持8m/s的速度跑完全程。设乙从起跑后到接棒前的运动是匀加速的，加速度大小为2.5m/s2. 乙在接力区前端听到口令时起跑，在甲乙相遇时完成交接棒.在某次练习中，甲以v=8m/s的速度跑到接力区前端s0=11.0m处向乙发出起跑口令.已知接力区的长度为L=20m.求：

（1）此次练习中交接棒处离接力区前端的距离.
（2）为了达到理想成绩，需要乙恰好在速度达到与甲相同时被甲追上，则甲应在接力区前端多远时对乙发出起跑口令？
（3）在（2）中，棒经过接力区的时间是多少？

参考答案：（12分）（1）5m（2）12.8m（3）2.5s

本题解析：（12分）（1）设乙加速到交接棒时运动时间为t，则在甲追击乙过程中有
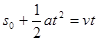?（2分）
代入数据得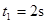?（1分）
（不符合乙加速最长时间3.2s实际舍去）?
此次练习中交接棒处离接力区前端的距离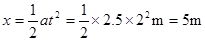（1分）
（2）乙加速时间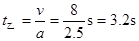?（2分）
设甲在距离接力区前端为s时对乙发出起跑口令，则在甲追击乙过程中有
?（2分）
代入数据得?（2分）
（3）棒在（2）过程以v=8m/s速度的运动，所以
棒经过接力区的时间是?（2分）
本题考查匀变速直线运动的追击和相遇问题，由两个运动员的运动性质列出位移方程，追上时位移相同，从而求得运动时间，再求得练习中交接棒处离接力区前端的距离，由匀变速直线运动的速度与时间的关系可求得乙的加速时间，恰好追上的临界条件是两人速度相同，由位移相同的等量关系可求得甲应在接力区前端距离
点评：追击和相遇问题最关键的是找出时间和位移的等量关系，速度相同是追的上或追不上的临界条件

本题难度：一般

4、选择题  如图3所示，处在平直轨道上的甲乙两物体相距s，同时同向开始运动，甲以初速度v加速度a1做匀加速运动，乙做初速度为零，加速度为a2的匀加速运动，假设甲能从乙旁边通过，下述情况可能发生的是（?）

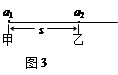
A a1 = a2时能相遇两次? B ?a1 > a2时能相遇两次
C ?a1 < a2时能相遇两次? D a1 < a2时能相遇一次

参考答案：C

本题解析：a1 = a2时相对加速度为零，以乙为参考系，甲做匀速直线运动，所以只能相遇一次，A错；a1 < a2，相遇时甲的速度大于乙的速度，以后乙的速度肯定能超过甲的速度，会再次相遇，C对；a1 > a2时相遇时刻甲的速度较大，此后乙不可能追上甲，只能相遇一次，B错；

本题难度：一般

5、选择题  甲、乙两车同时由静止从A点出发，沿直线AC运动.甲先以加速度a1做初速度为零的匀加速运动，到达B点后做加速度为a2的匀加速运动，到达C点时的速度为v；乙以加速度a3做初速度为零的匀加速运动，到达C点时的速度亦为v.若a1≠a2≠a3，则?（?）
A．甲、乙有可能同时由A到达C
B．甲、乙不可能同时由A到达C
C．甲一定先由A到达C
D．若a1＞a3，则甲一定先由A到达C

参考答案：BD

本题解析：略

本题难度：简单