1、简答题  如图所示，电阻忽略不计的两根两平行光滑金属导轨竖直放置，其上端接一阻值为3Ω的电阻R．在水平虚线L1、L2间有一与导轨所在平面垂直的匀强磁场B，磁场区域的高度为d=0.5m．导体棒a的质量ma=0.2kg、电阻Ra=3Ω；导体棒b的质量mb=0.1kg、电阻Rb=6Ω，它们分别从图中M、N处同时由静止开始沿导轨向下滑动，且都能匀速穿过磁场区域，当b?刚穿出磁场时a正好进入磁场．（不计a、b之间的作用）求：
（1）在整个过程中，a棒和b棒分别克服安培力做了多少功？
（2）在b穿过磁场区域过程中，电阻R产生的电热；
（3）M点和N点距L1的高度分别为多少？

参考答案：（1）因为两金属棒都是匀速穿过磁场的，所以安培力与重力等大，克服安培力做功分别为：Wa=magd=0.2×10×0.5J=1J
? Wb=mbgd=0.1×10×0.5J=0.5J
（2）设b切割磁感线时，其上电流为I，则电阻R和a棒上电流均为12I，根据焦耳定律：Q=I2Rt得：
? Qb：Qa：QR=I2Rbt：(I/2)2Rat：(I/2)2Rt=8：1：1
由（1）知b棒穿过磁场过程产生的总电热为Q=0.5J
所以：QR=18+1+1Q=0.05J
（3）b在磁场中匀速运动时：速度为υb，总电阻R1=7.5Ω．
b中的电流Ib=BLυbR1①
由以上各式得：B2L2υbR1=mbg②
a在磁场中匀速运动时：速度为va，总电阻R2=5Ω．
对a棒同理有：B2L2υaR2=mag③
由②③式得，υbυa=34④
又：υa=υb+gt⑤d=υbt⑥
由④⑤⑥得：v2a=16gd3，v2b=3gd
所以：ha=v2a2g=83d=83×0.5m≈1.33m
hb=v2b2g=1.5d=1.5×0.5m=0.75m
答：（1）在整个过程中，a棒和b棒分别克服安培力做功1J和0.5J．
（2）在b穿过磁场区域过程中，电阻R产生的电热是0.05J；
（3）M点和N点距L1的高度分别为1.33J和0.75J．

本题解析：

本题难度：一般

2、计算题  两金属杆ab和cd长均为l，电阻均为R，质量分别为M和m，M＞m，用两根质量和电阻均可忽略的不可伸长的柔软导线将它们连成闭合回路，并悬挂在水平、光滑、不导电的圆棒两侧，两金属杆都处在水平位置，如图4－93所示，整个装置处在一个与回路平面相垂直的匀强磁场中，磁感应强度为B．若金属杆ab正好匀速向下运动，求其运动的速度．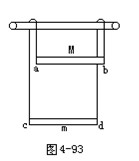

参考答案：v=(M-m)gR/2b2l2

本题解析：设磁场方向垂直纸面向里．由于M＞m，所以ab将向下，cd向上同作加速运动．由于ab和cd切割磁感线，分别产生感应电动势ε1和ε2，在回路中产生感应电流i，同时ab受到向上的安培力f，cd受到向下的安培力f，随着两杆运动速度增大，安培力f也增大，当两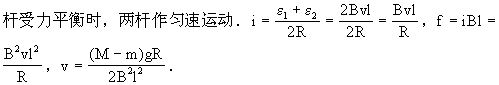

本题难度：一般

3、选择题  发现电磁感应现象的科学家是：
A．安培
B．奥斯特
C．法拉第
D．楞次

参考答案：C

本题解析：略

本题难度：一般

4、选择题  如图所示，大小相等的匀强磁场分布在直角坐标系的四个象限里，相邻象限的磁感强度B的方向相反，均垂直于纸面，现在一闭合扇形线框OABO，以角速度ω绕Oz轴在xOy平面内匀速转动，那么在它旋转一周的过程中(从图中所示位置开始计时)，线框内感应电动势与时间的关系图线是：
?

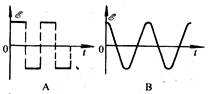
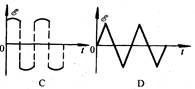
参考答案：A

本题解析：略

本题难度：简单

5、选择题  线框长为a，宽为b在磁感强度为B的匀强磁场中由图所示位置起绕OO′轴以角速度ω匀速转动，则t时刻感应电动势为

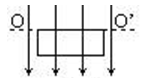
A.Babω·cosωt
B.Babω·sinωt
C.2Babω·sinωt
D.2Babω·cosωt

参考答案：A

本题解析：以OO′轴以角速度ω匀速转动，则长为a的边切割磁感线，其速度为：
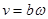，设转过一定角度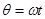，则改变上产生的感应电动势为：
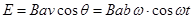，因此正确结果为A选项。
思路分析：线框只有一条边切割磁感线，求出该边切割磁感线时的感应电动势，要注意当该边转动时，速度方向和磁场方向不垂直则必须考虑将速度方向沿磁场方向和垂直磁场方向分解，沿磁场方向不产生电动势。
试题点评：本题是考查应用直导线切割磁感线时感应电动势的计算公式，特别要注意它的使用条件。

本题难度：困难