1、计算题  一辆值勤的警车停在公路边，当警员发现从他旁边以10?m/s的速度匀速行驶的货车严重超载时，决定前去追赶，经过5.5?s后警车发动起来，并以2.5?m/s2的加速度做匀加速运动，但警车的行驶速度必须控制在90km/h 以内。问：
（1）警车在追赶货车的过程中，两车间的最大距离是多少？
（2）警车发动后要多长时间才能追上货车？

参考答案：解：
（1）当两车速度相等时，它们的距离最大，设警车发动后经过t1时间两车的速度相等．则：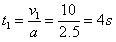
s货=v1(t0+t1)==10(5.5+4)m = 95m
s警
所以两车间的最大距离△s=s货-s警=75m；
（2）警车刚达到最大速度v=90km/h=25m/s的时间： t =
t内两车的位移
，
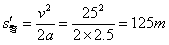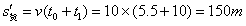
t时刻两车距离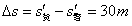
警车达到最大速度后做匀速运动，设再经过△t时间追赶上货车，
则：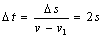
所以警车发动后要经过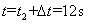才能追上货车。

本题解析：

本题难度：一般

2、选择题  如图所示，以8 m/s匀速行驶的汽车即将通过路口，绿灯还有2 s将熄灭，此时汽车距离停车线18 m。该车加速时最大加速度大小为2 m/s2，减速时最大加速度大小为5 m/s2。此路段允许行驶的最大速度为1 2.5 m/s。下列说法中正确的有

[? ]

参考答案：AC

本题解析：

本题难度：一般

3、选择题  从静止开始做匀加速直线运动的物体，第1s?内通过的位移为0.3m，则（　　）
A．第ls末的速度为0.3m/s
B．第2s内通过的位移是1.2m
C．加速度为0.6m/s2
D．前2s内的平均速度是l.2m/s

参考答案：C

本题解析：

本题难度：简单

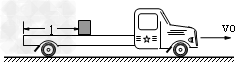
4、计算题  如图所示，一平板车以某一速度v0=5 m/s匀速行驶，某时刻一货箱（可视为质点）无初速度地放置于平板车上，货箱离车后端的距离为l= m，货箱放到车上的同时，平板车开始刹车，刹车过程可视为做a1=3 m/s2的匀减速直线运动。已知货箱与平板车之间的 摩擦因数为μ=0.2，g=10 m/s2。求：
（1）通过计算，判断货箱能否从车后端掉下来；
（2）如果货箱不能掉下，则最终停止时离车后端的距离d是多少；
（3）如果货箱不能掉下，最后都停止运动，平板车再从静止开始以a2=4 m/s2的加速度匀加速直线运动，经过3秒货箱距离车后端多远？已知平板车后端离地面高1.25 m，货箱落地后不动。?

参考答案：解：（1）货箱放到车上后，先做匀加速运动，设经过时间t和车达到相同速度，此时货箱和车的位移分别为x1、x2
对货箱：μmg=ma1，a1t?=v0-at，x1=v0t-a1t2
对平板车：x2=v0t-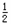at2
此时，货箱相对车向后移动了△x=x2-x1=2.5 m<l=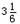 m，故货箱不会从车后端掉下来
（2）由于货箱的最大加速度a1=μg=2 m/s2<a，所以二者达到相同速度后，分别以不同的加速度匀减速运动到停止，此时相同速度为v=a1t=2 m/s?
对货箱：s1=v2/2a1=1 m?
对平板车：s2=v2/2a=2/3?m
故货箱到车尾的距离d1=l-△x+s1-s2=1 m
（3）设经过时间t1货箱和车分离，由位移关系得：d1=a2t12-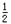a1t12?
解得t1=1 s
分离时货箱速度v1=a1t1=2 m/s，货箱做平抛运动，经过时间t2落地
∴h=gt22，得t2=0.5 s
则在平板车启动的t3=3 s内，货箱的水平位移x1"=a1t12+v1t2=2 m
平板车的位移为：x2"=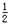a2t32=18 m
故货箱离平板车后端的距离：d2=x2"-x1"-d1=15 m

本题解析：

本题难度：一般

5、选择题  某质点做直线运动的位移x与时间t的关系为x=3t+t2（各物理量均采用国际单位），则该质点（   ）
A．第1s内的位移是3m
B．任意1s内的速度增量都是2m/s
C．前2s内的平均速度是6m/s
D．任意相邻的ls内位移之差都是1m