1、计算题  某人在地面上用弹簧秤称得其体重为490 N．他将弹簧秤移至电梯内称，0至9s时间段内电梯由静止开始运动，弹簧秤的示数如图所示，求电梯在这9s内的位移。

参考答案：18m, 方向向下

本题解析：由图知在0-3s内人处于失重状态，所以电梯向下做匀加速直线运动，得到，，，，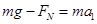
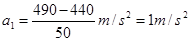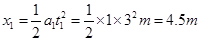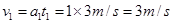
在3-6s内人处于正常状态，所以电梯向下做匀速直线运动，得到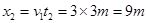
在6-9s内人处于超重状态，所以电梯向下做匀减速直线运动，得到，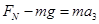
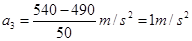
因，所以电梯在9s末速度恰好减为零，即
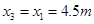
电梯在这9s内的位移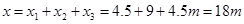
点评：学生应根据图像分析出电梯在各时间段的运动性质，再由匀变速直线运动的公式求出相应的物理量。

本题难度：简单

2、选择题  由牛顿第二定律可知，无论怎样小的力都可以使物体产生加速度。开始当我们用较小的力去推教室里的讲台时，却推不动它，这是因为　
A．牛顿第二定律不适用于静止物体
B．桌子的速度变化很小，不易察觉到
C．推力小于静摩擦力，加速度是负的
D．桌子所受合力为零

参考答案：D

本题解析：A、当水平的推力小于等于桌子受到的最大静摩擦力时，推力与桌子所受的静摩擦力平衡，合力为零，加速度为零，牛顿定律同样适用．
B、桌子的合力为零，根据牛顿第二定律没有产生加速度．
C、桌子没有被推动，速度没有变化，加速度为零，合力为零．
D、桌子静止，推力等于于桌子受到的摩擦力．

本题难度：简单

3、计算题  如图甲，在水平地面上固定一倾角为θ的光滑绝缘斜面，斜面处于电场强度大小为E、方向沿斜面向下的匀强电场中。一劲度系数为k的绝缘轻质弹簧的一端固定在斜面底端，整根弹簧处于自然状态。一质量为m、带电量为q（q>0）的滑块从距离弹簧上端为s0处静止释放，滑块在运动过程中电量保持不变，设滑块与弹簧接触过程没有机械能损失，弹簧始终处在弹性限度内，重力加速度大小为g。
（1）求滑块从静止释放到与弹簧上端接触瞬间所经历的时间t1；
（2）若滑块在沿斜面向下运动的整个过程中最大速度大小为vm，求滑块从静止释放到速度大小为vm过程中弹簧的弹力所做的功W；
（3）从滑块静止释放瞬间开始计时，请在乙图中画出滑块在沿斜面向下运动的整个过程中速度与时间关系v-t图象。图中横坐标轴上的t1、t2及t3分别表示滑块第一次与弹簧上端接触、第一次速度达到最大值及第一次速度减为零的时刻，纵坐标轴上的v1为滑块在t1时刻的速度大小，vm是题中所指的物理量。（本小题不要求写出计算过程）

参考答案：解：（1）滑块从静止释放到与弹簧刚接触的过程中作初速度为零的匀加速直线运动，设加速度大小为a，则有
qE+mgsin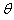=ma ①
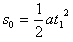?②
联立①②可得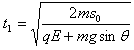 ③
（2）滑块速度最大时受力平衡，设此时弹簧压缩量为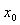，则有
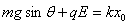?④
从静止释放到速度达到最大的过程中，由动能定理得
?⑤
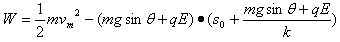联立④⑤可得s
（3）如图

本题解析：

本题难度：困难

4、填空题  火车质量为5×105kg，在运动过程中受到的阻力与速度的平方成正比，即Ff=kv2，其中k=5×102kg/m．在火车从甲地开出向乙地直线运行的过程中，开始阶段做匀加速直线运动，加速度大小为0.3m/s2，则当速度达到36km/h时，火车牵引力的大小是______N．

参考答案：速度是36km/h=10m/s时的阻力：Ff=kv2=5×102×102=5×104N
根据牛顿第二定律得：ma=F-Ff
所以：F=Ff+ma=5×104+5×105×0.3=2.0×105N
故答案为：2×105．

本题解析：

本题难度：一般

5、选择题  如图所示，在光滑绝缘水平面上，两个带等量正电的点电荷M、N，分别固定在A、B两点，O为AB连线的中点，CD为AB的垂直平分线．在CO之间的F点由静止释放一个带负电的小球P（设不改变原来的电场分布），在以后的一段时间内，P在CD连线上做往复运动．若（　　）
A．小球P的带电量缓慢减小，则它往复运动过程中振幅不断减小
B．小球P的带电量缓慢减小，则它往复运动过程中每次经过O点时的速率不断减小
C．点电荷M、N的带电量同时等量地缓慢增大，则小球P往复运动过程中周期不断减小
D．点电荷M、N的带电量同时等量地缓慢增大，则小球P往复运动过程中振幅不断减小