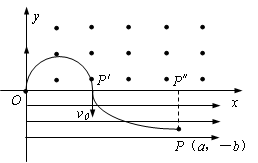
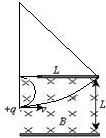
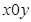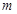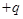1、计算题  （14分）如图所示，在直角坐标系内，有一质量为,电荷量为的粒子A从原点O沿y 轴正方向以初速度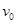射出，粒子重力忽略不计，现要求该粒子能通过点P(a, -b),可通过在粒子运动的空间范围内加适当的“场”实现。

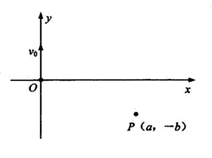
(1) 若只在整个I、II象限内加垂直纸面向外的匀强磁场，使粒子A在磁场中作匀速圆周运动，并能到达P点，求磁感应强度B的大小；
(2) 若只在x轴上某点固定一带负电的点电荷Q, 使粒子A在Q产生的电场中作匀速圆周运动，并能到达P点，求点电荷Q的电量大小；
(3) 若在整个I、II象限内加垂直纸面向外的匀强磁场，并在第IV象限内加平行于x轴，沿x轴正方向的匀强电场，也能使粒子A运动到达P点。如果此过程中粒子A在电、磁场中运动的时间相等，求磁感应强度B的大小和电场强度E的大小

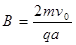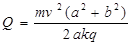参考答案：（1）（2）（3），

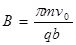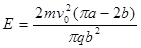
本题解析：（1）粒子由O到P的轨迹如图所示，粒子在磁场中做圆周运动，半径为R1,由几何关系知

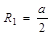?（1分）
由牛顿第二定律可知：
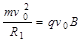?（1分）
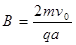由此得?（1分）
（2）粒子由O到P的轨迹如图所示

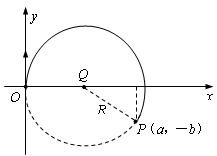
粒子在电场中做圆周运动，半径为R2：
由几何关系知：

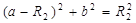
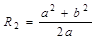?（2分）
由牛顿第二定律可知
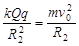?（1分）
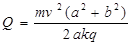由此得：?（1分）
（3）粒子由O经P＇到P的轨迹如图所示，在磁场中做圆周运动，在电场中做类平抛运动
在电场中运动时间t：

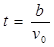?（1分）
在磁场中运动时间t：
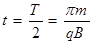?（1分）
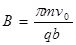由此得：?（1分）
设在磁场中做圆周运动，半径为R3
则有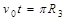?（1分）

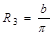
电场中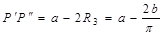?（1分）
?（1分）
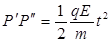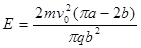由此得?（1分）

本题难度：一般

2、计算题  （18分）
如图15所示，PQ、MN两极板间存在匀强电场，两极板间电势差为U、间距为d，MN极板右侧虚线区域内有垂直纸面向内的匀强磁场。现有一初速度为零、带电量为q、质量为m的离子从PQ极板出发，经电场加速后，从MN上的小孔A垂直进入磁场区域，并从C点垂直于虚线边界射出。求：
（1）离子从小孔A射出时速度v0；
（2）离子带正电还是负电？C点离MN板的距离？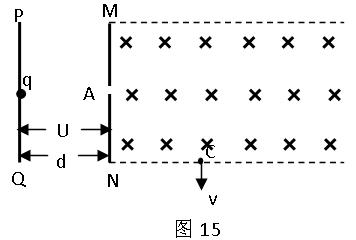

参考答案：（1）
（2）

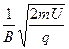
本题解析：（1）由动能定理得：qU=?（4分）
解得离子从小孔A射出时速度v0=?（4分）
注：用牛顿第二定律求解同样给分
（2）由左手定则可知离子带负电（3分）。

离子进入磁场后，洛仑兹力提供向心力，由
牛顿第二定律：qv0B=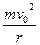（3分）
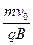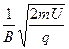解得：r==?（4分）
所以C点离MN板的距离为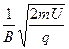

本题难度：简单

3、选择题  长为L的水平板间，有垂直纸面向内的匀强磁场，如图所示，磁感应强度为B，板间距离也为L，板不带电，现有质量为m，电量为q的带正电粒子（不计重力），从左边极板间中点处垂直磁感线以速度v水平射入磁场，欲使粒子打在极板上，可采用的办法是（　　）
A．使粒子的速度v＜

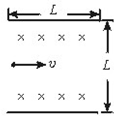
参考答案：如图所示，由题意知，带正电的粒子从左边射出磁场，其在磁场中圆周运动的半径R＜L4，故粒子在磁场中做圆周运动洛伦兹力提供向心力即：qvB=mv2R
可得粒子做圆周运动的半径：R=mvqB
粒子不从左边射出，则：mvqB＞L4
即：v＞qBL4m
带正电的粒子不从右边射出，如图所示，此时粒子的最大半径为R，由上图可知：R2=L2+（R-L2）2
可得粒子圆周运动的最大半径：R=5L4
又因为粒子做圆周运动，洛伦兹力提供向心力，粒子不从右边射出，则：mvqB＜5L4
即：v＜5qBL4m
故欲使粒子打在极板上，粒子的速度必须满足BqL4m＜v＜5BqL4m，故D正确
故选：D

本题解析：

本题难度：简单

4、选择题  如图所示，在真空中一条竖直向下的电场线上有a、b两点．一带电质点在a处由静止释放后沿电场线向上运动，到达b点时速度恰好为零．则下面说法正确的是 (　　)

A．该带电质点一定带正电荷
B．a点的电场强度大于b点的电场强度、
C．a点的电场强度小于b点的电场强度
D．质点在b点所受到的合力一定为零

参考答案：B

本题解析：解答本题要掌握：根据质点的运动情况，正确判断其受力情况，弄清在a、b两点电场力和重力大小关系；
带电质点由a点释放后向上运动，可知合力方向向上，而质点所受重力竖直向下，故电场力一定竖直向上，与电场线方向相反，可知该质点一定带负电，故A项错误；
带电质点到b点时速度又减为零，可知向上运动过程中，合力先向上再向下，即重力不变，电场力减小，可知a处电场强度大于b处电场强度，B正确，CD错误
点评：解决带电粒子在复合场中的运动，要正确进行受力分析，确定其运动状态，然后依据相关规律求解．

本题难度：简单

5、简答题  如图所示，水平方向的匀强电场的场强为E，场区宽度为L，竖直方向足够长．紧挨着电场的是垂直于纸面向外的两个匀强磁场区域，其磁感应强度分别为B和2B．一个质量为m，电量为q的带正电粒子，其重力不计，从电场的边界MN上的a点由静止释放，经电场加速后进入磁场，经过时间tB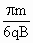＝穿过中间磁场，进入右边磁场后能按某一路径再返回到电场的边界MN上的某一点b，途中虚线为场区的分界面．求：

(1)中间场区的宽度d；
(2)粒子从a点到b点所经历的时间tab；
(3)当粒子第n次返回电场的MN边界时与出发点之间的距离sn．
?

参考答案：
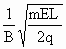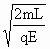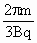（1）?（2）2＋? (3)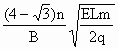

本题解析：粒子从a点出发，在电场中加速和在磁场中偏转，回到MN上的b点，轨迹如图所示

　　(1)粒子在电场中加速运动时，有
　　? qEL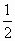＝mv2　　解得v＝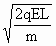
　　由tB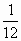＝T,得：粒子在中间磁场通过的圆弧所对的圆心角为θ＝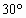
　　粒子在中间磁场通过的圆弧半径为r1＝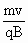
　　由几何关系得d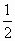＝r1＝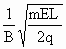
　　(2)粒子在右边磁场中运动：其圆弧对应的圆心角为α＝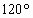
　　则t2B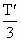＝＝　　粒子在电场中加速时：
Eq·tE＝mv　　tE＝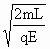
　　根据对称性：tab＋2tE＋2tB＋t2B＝2＋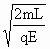
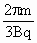
　　(3)由轨迹图得：y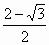＝r1－＝r1　
　Sab＝r1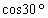＋2y＝(2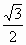－)r1
　　再由周期性：Sn＝nSab－(2－)＝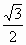

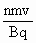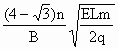
本题难度：一般