1、计算题  （16分） 如图所示，质量为1kg的小物块以5m/s的初速度滑上一块原来静止在水平面上的木板，木板质量为4kg，木板与水平面间的动摩擦因数为0.02，经时间2s后，小物块从木板另一端以1m/s相对于地的速度滑出，g=10m/s2，求这一过程中木板的位移和系统在此过程中因摩擦增加的内能.

参考答案：（16分）解:对小木块由动量定理得: μ1mgt = mv0 - mv1?①
对木板由动量定理得: μ1mgt –μ2(M+m)gt = Mv?②
由以上两式得: μ2(M+m)gt = mv0?- mv1?- Mv?③
解得v="0.5m/s?" ④
此过程中木板做匀加速运动，所以有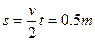?⑤
由能量守恒得:Q =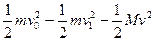=11.5J ?⑥

本题解析：略

本题难度：简单

2、计算题  有一个用直流电动机提升重物的装置，重物的质量m＝50 kg，电路电压为120 V，当电动机以v＝0.9 m/s的恒定速度向上提升重物时，电路中的电流I＝5 A，求：
(1)电动机线圈的电阻R等于多少？
(2)电动机对该重物的最大提升速度是多少？
(3)若因故障电动机不能转动，这时通过电动机的电流是多大，电动机消耗的电功率又为多大？(取g＝10 m/s2)

参考答案：解：(1)设电动机输入功率为P，输出功率为P1，热消耗功率为P2，则有
P＝P1＋P2＝mgv＋I2R
R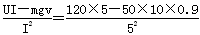＝Ω ＝6 Ω
(2)P1＝P－P2＝UI－I2R＝－R(I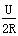－)2＋
当＝I时，P1有最大值为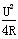
当I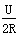＝＝10 A，电动机的输出最大功率P1大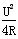＝＝600 W
由于P1大＝mgv大，有v大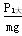＝＝1.2 m/s
(3)因电动机不能转动，此时电路中电流最大，最大电流为I大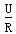＝＝20 A
电动机消耗的功率也最大P2大＝I2大R＝2400 W

本题解析：

本题难度：一般

3、选择题  如图所示，固定的倾斜光滑杆上套有一个质量为m的圆环，圆环与竖直放置的轻质弹簧一端相连，弹簧的另一端固定在地面上的A点，弹簧处于原长h时，让圆环由静止开始沿杆滑下，滑到杆的底端时速度恰好为零。若以地面为参考面，则在圆环下滑过程中

[? ]
A.圆环的机械能保持为mgh?
B.弹簧的弹性势能先增大后减小
C.弹簧弹力做的功为－mgh
D.弹簧的弹性势能最大时，圆环的动能和重力势能之和最小

参考答案：CD

本题解析：

本题难度：一般

4、选择题  北京时间2012年2月18日，中国“飞人”刘翔在伯明翰国际田联大奖赛男子60米跨栏比赛中，以7秒41的成绩夺冠，创造今年世界最好成绩!比赛中他采用蹲踞式起跑，在发令枪响后，左脚迅速蹬离起跑器，在向前加速的同时提升身体重心，如图所示．假设刘翔的质量为m，在起跑时前进的距离s内，重心升高量为h，获得的速度为v，阻力做功为W阻，则在此过程中

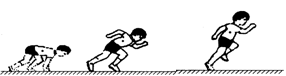
A．运动员的机械能增加了
B．运动员所受的合外力做功为
C．运动员的重力做功为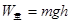
D．运动员自身做功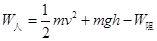

参考答案：AD

本题解析：机械能等于动能与势能之和，在起跑时动能增加了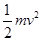，重力势能增加了mgh，所以机械能增加了，选项A正确；由动能定理可知选项B错误；运动员的重力做功为；选项C错误；根据能量守恒定律可知选项D正确；故选AD
点评：本题难度中等，在运动员起跑时，不但自身做功，起跑器也要释放弹性势能做功

本题难度：一般

5、选择题 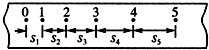 利用打点计时器测定物体做匀变速直线运动的加速度时，在纸带上打出一系列的点，如图所示，设各相邻计数点之间的距离分别为s1、s2、s3、s4，相邻两计数点的时间间隔为T，则下列关系式中正确的是
A.s2-s1=aT2
B.s4-s1=3aT2
C.打点2时物体的速度为v2=
D.

参考答案：ABC

本题解析：分析：根据匀变速直线运动中时间中点的速度等于该过程中的平均速度，可以求出打纸带上2点时小车的瞬时速度大小．
根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小．
解答：A、根据匀变速直线运动的推论得：相邻的相等的时间间隔位移之差相等．
即根据△x=aT2得，s2-s1=aT2，故A正确．
s4-s1=3aT2，故B正确．
C、根据匀变速直线运动中时间中点的速度等于该过程中的平均速度得，
打点2时物体的速度为v2=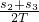．故C正确．
D、计数点0点不一定是打出的第一个点，所以0点的速度不一定等于零，
所以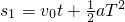，故D错误．
故选ABC．
点评：要提高应用匀变速直线的规律以及推论解答实验问题的能力，在平时练习中要加强基础知识的理解与应用．

本题难度：一般