1、计算题  （8分）如图所示，在与水平方向成θ角的光滑金属导轨间连一电源，在相距L的平行导轨上放一质量为m的金属棒ab，棒上通过的电流为I，磁场方向竖直向上，这时金属棒恰好静止，则：

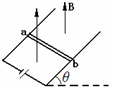
（1）匀强磁场的磁感强度为多大？
（2）欲使导体棒静止在导轨上，求外加的匀强磁场的磁感应强度的最小值及方向。

参考答案：(1)   (2)，方向垂直于斜面向上

本题解析：（1）由力的平衡条件可得：BIL =" mgtanθ" （2分）
解得：    （1分）
（2）当磁感应强度垂直于斜面向上时，磁感应强度最小（2分）
BmIL= mgsinθ      （2分）
解得     （1分）
考点：本题考查了力的平衡、安培力.

本题难度：一般

2、选择题  关于磁感应强度的概念，以下说法中正确的有（　　）
A．电流元IL在磁场中受力为F，则磁感应强度B一定等于

参考答案：A、只有当电流元与磁场垂直时，B=FIL．当电流元与磁场垂直不时，B≠FIL．故A错误．
? B、当电流元与磁场垂直不时F=BILsinα，α是电流元与磁场方向的夹角．则B≥FIL．故B正确．
? C、由公式F=BILsinα可知，磁场中电流元受力情况取决于B、I、L及α四个因素，则F大，B不一定大．故C错误．
? D、磁感应强度的方向，与电流元在此点的受力方向垂直．故D错误．
故选B．

本题解析：

本题难度：简单

3、选择题  一条竖直放置的长直导线，通以由下向上的电流，在它正北方某点的磁场方向为（ ?）
A．向东．　　
B．向西．
C．向南．
D．向北．

参考答案：B

本题解析：安培定则，安培定则，也叫右手螺旋定则，是表示电流和电流激发磁场的磁感线方向间关系的定则。通电直导线中的安培定则（安培定则一）：用右手握住通电直导线，让大拇指指向电流的方向，那么四指的指向就是磁感线的环绕方向；通电螺线管中的安培定则（安培定则二）：用右手握住通电螺线管，使四指弯曲与电流方向一致，那么大拇指所指的那一端是通电螺线管的N极。
由安培定则可以判断，B项正确，故选B。
点评：理解掌握安培定则，并会应用判断直线电流和环形电流的磁场方向。

本题难度：简单

4、选择题  如图所示为磁场中某区域的磁感线分布，则( ?)

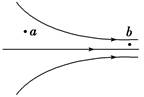
A．a、b两处的磁感应强度的大小不等，Ba＞Bb
B．a、b两处的磁感应强度的大小不等，Ba＜Bb
C．同一电流元放在a处受力可能比放在b处受力大
D．同一电流元放在a处受力一定比放在b处受力小

参考答案：BC

本题解析：AB、同一磁场中磁感线的疏密表示磁场的强弱，磁感线越密的地方磁场越强，磁感线越疏的地方磁场越弱。由图A错误；B正确
CD、同一电流元在磁场中某点受力的大小，除了与磁场强弱有关外，还与导线的方向有关．导线放入磁场中的方向不同，所受磁场力也不相同。所以，C正确，D 错误
故选BC
点评：容易题。定义式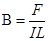成立的条件是：通电导线必须垂直于磁场方向放置．

本题难度：一般

5、计算题  磁感应强度为矢量，它可以分解为几个分量。
(1)如果北半球某处地磁场的磁感应强度大小为B，与水平方向的夹角为θ且斜向下，那么该处地磁场的磁感应强度的水平分量和竖直分量各为多大？
(2)如果地理南、北极和地磁北、南极是重合的，那么在赤道上空磁场的竖直分量是多大？在极地上空地磁场的水平分量是多大？

参考答案：(1)Bx＝Bcosθ　By＝Bsinθ　(2)By＝0　Bx＝0

本题解析：(1)如图所示磁感应强度大小为B，与水平方向的夹角为θ，所以地磁场的磁感应强度的水平分量和竖直分量分别为：Bx＝Bcosθ，By＝Bsinθ。

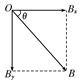
(2)在赤道上空，因为θ＝0°，故有By＝0；在极地上空，因为θ＝90°，故有Bx＝0。
点评：关键是知道磁感应强度是矢量，相加减遵循平行四边形定则

本题难度：简单