1、简答题  如图所示，在y≤5

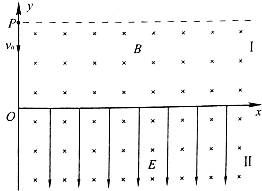
参考答案：（1）带电粒子进入区域I中，由洛伦兹力充当向心力，则有


? qv0B=mv20r
得 r=mv0qB
代入数据解得，r=0.1m=10cm
由几何知识得：x=r（1-cos60°）=5cm
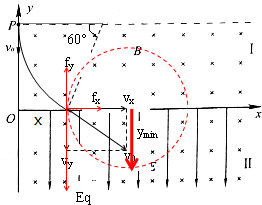
（2）如图，带电粒子进入区域Ⅱ时，将速度v0分析为水平和竖直两个分速度vx和vy．与两个分速度对应的洛伦兹力分力分别为fy和fx．
则得fy=qvxB=qv0cos30°B，电场力F=Eq，
代入解得，fy=qvyB=mv2yR
解得，R=mvyqB=5cm
所以带电粒子在区域Ⅱ中到达最低点的纵坐标ymin=-R=-5cm．
（3）带电粒子从进入区域I开始到第二次穿越x轴时经过的时间t=tⅠ+tⅡ=16T+12T=23T=23×2πmqB
代入解得，t=2.1×10-5s
答：
（1）带电粒子第一次穿越X轴时的横坐标x是5cm；
（2）带电粒子在区域Ⅱ中到达最低点的纵坐标y是-5cm．
（3）带电粒子从进入区域I开始到第二次穿越x轴时经过的时间t是2.1×10-5s．

本题解析：

本题难度：一般

2、计算题  如图所示，半径为R、内径很小的光滑半圆轨道竖直放置在水平地面上，两个质量为m的小球A、B（直径略小于管内径），以不同速度进入管内。A通过轨道的最高点C时，对管壁恰好无弹力的作用。A、B两球落地点的水平距离为4R，求：B球在最高点C对管壁的弹力大小和方向?（两球离开管后在同一竖直面内运动）

参考答案：B球在最高点C对管壁的弹力大小为2mg、方向竖直向上

本题解析：：（1）设a、b两球通过半圆管最高点A时的速度分别为va、vb，圆周运动知识可知：对a球 mg=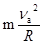va=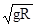
a、b两球通过半圆管最高点A后，做平抛运动，设运动时间为t，落地间后的间距为4R，
2R=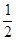gt2?4R=vbt-vat ?解得：vb=3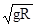
对b球在C点有：mg+F=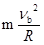? F=8mg，方向向下
点评：本题是向心力知识和平抛运动的综合应用，常规题，考试时不能失误．

本题难度：简单

3、简答题  为了迎接2008年北京奥运会的召开，我市某校的物理兴趣小组设计了如图所示的玩具轨道，其中“2008”四个等高数字是用内壁光滑的薄壁细圆玻璃管弯成，固定在竖直平面内（所有数字均由圆形和直圆管组成，P点与M、N点等高，圆半径比细管的内径大得多），底端与水平地面相切．右端的弹射装置将一个小球（小球的直径略小于玻璃管的内径，且可以视为质点），以va=5m/s的水平初速度由a点弹出，从b点进入玻璃轨道，依次经过“8002”后从p点水平抛出．设小球与地面ab段间的动摩擦因数u=0.3，不计其它机械能损失．已知ab段长x=1.5m，数字“0”的半径R=0.2m，小球的质量m=0.01kg，取g=10m/s2．试求：

（1）小球运动到数字“8”的最高点N处和数字“0”的最高点M处的角速度之比．
（2）小球到达数字“8”的最高点N时管道对小球作用力的大小和方向．
（3）小球从p点抛出后落到地面时的速度．

参考答案：（1）由机械能守恒定律知，小球在M和N两点的速度相同，由公式v=ωr得两点的角速度之比为ωNωM=RMRN=21
（2）小球由位置a经b运动到N点的过程，应用动能定理得：μmgx+mg×2R=12mv2a-12mv2N
v2N=v2a-4gR-2μgx=52-4×10×0.2-2×0.3×10×1.5=8?
设小球在N点轨道给它的压力为FN，由牛顿第二定律得FN+mg=mv2NR/2
FN=2mv2NR-mg=2×0.01×80.2-0.01×10=0.7(N)
方向竖直向下?
（3）由机械能守恒定律知，小球过P点以速度vP=vN=

本题解析：

本题难度：一般

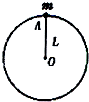
4、选择题  长度为L=0.50m的轻质细杆OA，A端有一质量为m=2.0kg的小球，如图所示，小球以O点为圆心在竖直平面内做圆周运动，不计各种摩擦，小球在最低点时的速率是6.0m/g取10m/s2，则小球最高点时细杆OA受到（　　）
A．64N的拉力
B．64?N的压力
C．44N的拉力
D．144?N的拉力