1、简答题 某同学在探究物体弹性碰撞的特点时,先提出了如下假设:①两个物体碰撞前后各自的质量与自己的速度的乘积之和是不变的;②两个物体碰撞前后各自的质量与自己速度的二次方的乘积之和是不变的.为了验证这个假设,该同学设计了如图1所示的实验装置.先将弹性a球从斜槽轨道上某固定点处由静止开始滚下,在水平地面上的记录纸上留下压痕,重复10次;再把同样尺寸大小的弹性b球放在斜槽轨道末端水平段的最右端附近静止,让a球仍从原固定点由静止开始滚下,和b球相碰后,两球分别落在记录纸的不同位置处,重复10次.
(1)在安装斜槽轨道时,要注意______.选择弹性小球a、b时,小球a、b的质量ma、mb应该满足关系:ma______mb(填“>”或“=”或“<”),理由是______.
(2)本实验必须测量的物理量有以下哪些______.
A.斜槽轨道末端到水平地面的高度H
B.小球a、b的质量ma、mb
C.小球a、b的半径r
D.小球a、b?离开斜槽轨道末端后平抛飞行时间t
E.记录纸上O点到A、B、C各点的距离SOA、SOB、SOC
F.a球的固定释放点到斜槽轨道末端水平部分间的高度差h
(3)该同学设计了一个实验数据表格,见表一.从表中可以看出,有些物理量并非实验中直接测出的,请你将表中不能直接测出的物理量换成能直接测出的物理量,而不影响实验探究的目的,并将结果对应填在表二中.
表一:
| 碰撞前 | 碰撞后
|
质量
ma
ma
mb
|
速度
va
v’a
v’b
|
mv
mava | mav’a+mbv’b
|
|
mv2
mav2a | mav’2a+mbv’2b
|
|
表二:
(4)为测定未放被碰小球时,小球a落点的平均位置,把刻度尺的零刻线跟记录纸上的O点对齐,图2给出了小球a落点附近的情况,由图可得OB距离应为______cm.
(5)该同学通过对实验数据的分析和处理验证了他的假设,这就表明物体在弹性碰撞中有两个物理量是守恒的,这两个物理量分别是______、______.
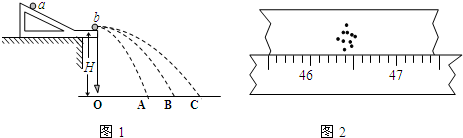
参考答案:(1)在安装斜槽轨道时,要注意调整斜槽末端水平,保证小球做平抛运动.选择弹性小球a、b时,入射小球的质量大于被碰小球的质量,防止入射小球反弹.
(2)在实验中,需验证动量是否守恒,需测量两小球的质量,记录纸上O点到A、B、C各点的距离SOA、SOB、SOC,因为平抛运动的时间相等,水平距离的大小代表速度的大小.故选BE.
(3)小球碰撞前后的速度可以通过平抛运动的水平位移代替,如表格所示.
(4)OB的距离为落点的平均位置,大小等于46.41cm.
(5)物体在弹性碰撞的过程中,系统动量守恒,机械能守恒.
故答案为:
(1)调整斜槽末端水平,>,防止入射小球反弹;
(2)B、E (3)见下表?
(4)46.41;(5)动量?机械能.
碰撞前碰撞后质量mamamb速度SoBSoAS0Cmvma?SoBmasoA+mbS0Cmv2maS2oBm?S2oA+mbS20C
本题解析:
本题难度:一般
2、计算题 试在下述简化情况下由牛顿定律导出动量守恒定律的表达式:系统是两个质点,相互作用力是恒力,不受其他力,沿直线运动,要求说明推导过程中每步的根据,以及式中各符号和最后结果中各项的意义.
参考答案: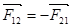
m2 =-m1
=-m1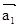
m2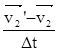 =-m1·
=-m1· 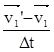
m1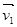 +m2
+m2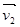 =m1
=m1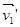 +m2
+m2
本题解析:略
本题难度:简单
3、选择题 质量为M的小车在光滑水平地面上以速度v0匀速向右运动,当车中的砂子从底部的漏斗中不断流下时,车子速度将(?)
A.减小
B.不变
C.增大
D.无法确定
参考答案:B
本题解析:砂子从底部的漏斗中不断流下时,由于惯性砂子也具有向右的速度v0,根据动量守恒定律得到 ,解得
,解得 ,所以车子速度不变,B对,ACD错。
,所以车子速度不变,B对,ACD错。
本题难度:简单
4、计算题 甲、乙两小船质量均为M=120 kg,静止于水面上,甲船上的人质量m=60 kg,通过一根长为L=10 m的绳用F=120 N的水平力拉乙船,求:
(1)两船相遇时,两船分别走了多少距离.
(2)为防止两船相撞,人至少以多大的速度跳离甲船.(忽略水的阻力)
参考答案::(1)4 m 6 m (2)4m/s
本题解析::(1)甲船和人与乙船组成的系统动量时刻守恒.
由平均动量守恒得:(M+m)x甲=Mx乙
又x甲+x乙=L
以上两式联立可求得:x甲=4 m,x乙=6 m.
(2)设两船相遇时甲船的速度为v1,对甲船和人用动能定理得:
Fx甲=(M+m)v
因系统总 动量为零,所以人跳离甲后,甲速度为零时,人跳离速度最小,设人跳离的速度为v,因跳离时,甲船和人组成的系统动量守恒,有:(M+m)v1=0+mv可求得:v=4m/s.
本题难度:一般
5、简答题 一质量为m、电荷量+q的与外界绝缘物块A(可视为质点),置于光滑水平面上.A与弹簧左端相连接,弹簧右端固定在竖直墙面上,整个空间中存在水平向右的匀强电场,场强为E,平衡时弹簧的压缩量为x0,如图O为弹簧原长时的位置,另一个质量也为m电量为+2q的绝缘带电物块B(可视为质点),从O点左侧距离O为7x0处的p点由静止释放,当它打在A物块上时立即与A一起向右运动,但不粘连,它们到达最右端后又向左运动,试求:物块B向左运动达到最远点时距O点的距离?(A、B相撞在瞬间完成,电荷无转移,不计A、B间库仑力,弹簧始终在弹性限度内).

参考答案:对A受力分析:qE=kx0
解得:k=qEx0
对B,由动能定理得:
2qE?8x0=12mv2
解得:v=4
本题解析:
本题难度:一般