1、选择题  如图所示，在垂直纸面向里的匀强磁场的边界上，有两个电荷量绝对值相同、质量相同的正、负粒子(不计重力)，从A点以相同的速度先后射入磁场中，入射方向与边界成θ角，则正、负粒子在磁场中(? )

A．运动时间相同
B．运动轨迹的半径相同
C．重新回到边界时速度大小和方向相同
D．重新回到边界时与A点的距离相等

参考答案：BCD

本题解析：
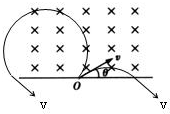正负离子垂直射入磁场后都做匀速圆周运动，根据牛顿第二定律研究轨道半径关系；根据圆的对称性分析重新回到磁场边界时正负离子速度大小和方向的关系；写出轨迹的圆心角，研究运动的时间关系；根据几何知识研究正负离子重新回到磁场边界的位置与O点距离关系。设正离子轨迹的圆心角为α，负离子轨迹的圆心角为β，由几何知识得到，α=2π-2θ，β=2θ，由粒子做圆周运动的周期公式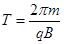知：负离子运动的时间为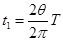，正离子运动的时间为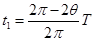，故两粒子运动时间不相同，则t1<t2．故A错误；正负离子垂直射入磁场后都做匀速圆周运动的半径为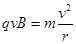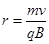，，由题意可知，正负离子质量、电荷量均相等，速度相同，B相同，则它们运动的轨道半径相同．故B正确；两个离子轨迹都是圆，速度是轨迹的切线方向，如图，根据圆的对称性可知，重新回到磁场边界时速度大小和方向都相同．故C正确； 根据几何知识得到，重新回到磁场边界的位置与O点距离相等．故D正确；本题故选ABD。带电粒子垂直射入单边有界的匀强磁场中，可分两类模型分析：一为同方向射入的不同粒子；二为同种粒子以相同的速率沿不同方向射入．无论哪类模型，都遵守以下规律：
（1）轨迹的圆心在入射方向的垂直线上，常可通过此垂线的交点确定圆心的位置．
（2）粒子射出方向与边界的夹角等于射入方向与边界的夹角．

本题难度：一般

2、简答题  


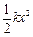
（1）求导体棒在磁场中做匀速运动的速度大小v0和弹簧的劲度系数k
（2）求导体棒最终停止位置距O点的距离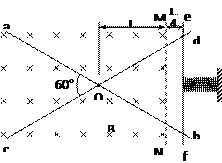

参考答案：
（1）（2）

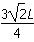
本题解析：
（1）由能量守恒，得：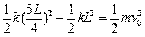

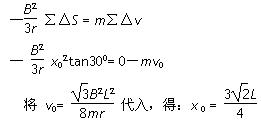
本题难度：一般

3、选择题  如图所示，边长为L的等边三角形ABC为两有界匀强磁场的理想边界，三角形内的磁场方向垂直纸面向外，磁感应强度大小为B，三角形外的磁场（足够大）方向垂直纸面向里，磁感应强度大小也为B。把粒子源放在顶点A处，它将沿∠A的角平分线发射质量为m、电荷量为q、初速度为v0的带电粒子（粒子重力不计）。若从A射出的粒子

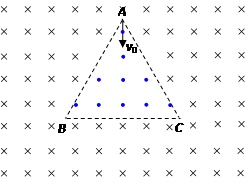
①带负电，，第一次到达C点所用时间为t1
②带负电，，第一次到达C点所用时间为t2
③带正电，，第一次到达C点所用时间为t3
④带正电，，第一次到达C点所用时间为t4
则下列判断正确的是（ ）
A．t1= t3< t2= t4          B．t1< t2< t4 < t3
C．t1< t2< t3< t4        D．t1< t3< t2< t4

参考答案：B

本题解析：若从A射出的粒子带负电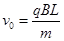，，向右偏转，其轨迹半径等于L，粒子周期设为T，第一次到达C点所用时间为t1=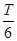；若从A射出的粒子带负电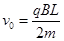，，向右偏转，其轨迹半径等于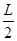，经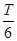后经过理想边界外向左偏转，再经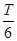后第一次到达C点所用时间为t2=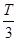，如图甲：

若从A射出的粒子带正电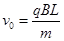，，向左偏转，其轨迹半径等于L，第一次到达B点所用时间为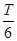，进入理想边界向右偏转，再经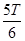后第一次到达C点，所用总时间为t3=T；若从A射出的粒子带正电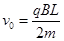，，向左偏转，其轨迹半径等于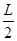，经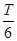后进入理想边界外向右偏转，再经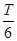后第一次到达B点所用时间为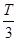，再经T后第一次到达C点，所用总时间为t4=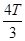，如图乙：

故选项B正确。
考点：带电粒子在磁场中的圆周运动

本题难度：一般

4、选择题  如图所示，宽h=2cm的有界匀强磁场，纵向范围足够大，磁感应强度的方向垂直纸面向内，现有一群正粒子从O点以相同的速率沿纸面不同方向进入磁场，若粒子在磁场中做匀速圆周运动的轨道半径均为r=5cm，则
[? ]

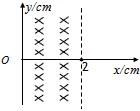
A．右边界：-4cm<y<4cm有粒子射出
B．右边界：y>4cm和y<-4cm有粒子射出
C．左边界：y>8cm有粒子射出
D．左边界：0<y<8cm有粒子射出

参考答案：AD

本题解析：

本题难度：一般

5、计算题  在如图所示的空间里，存在垂直纸面向里的匀强磁场，磁感应强度为.在竖直方向存在交替变化的匀强电场如图（竖直向上为正），电场大小为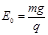．一倾角为θ足够长的光滑绝缘斜面放置在此空间．斜面上有一质量为m，带电量为-q的小球，从t=0时刻由静止开始沿斜面下滑，设第5秒内小球不会离开斜面，重力加速度为g

求：（1）求第1秒末小球的速度大小．
(2)第6秒内小球离开斜面的最大距离．
（3）若第19秒内小球仍未离开斜面，θ角应满足什么条件？

参考答案：（1）2g sinθ；（2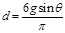）；（3）。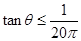

本题解析：（15分）考查动力学、圆周运动、静电场、磁场有关知识及临界问题，另考查学生在解题中寻找运动规律，综合性较强，考查内容较为深入．

解析(1)设第一秒内小球在斜面上运动的加速度为a,
由牛顿第二定律得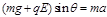：?①?（2分）
第一秒末的速度为：v=at1="2g" sinθ? (m/s)?②?（2分）
(2)在第二秒内：qE0=mg?③?（1分）
所以小球将离开斜面在上方做匀速圆周运动，则：
由牛顿第二定律得
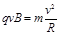?④?（1分）
圆周运动的周期为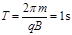：?⑤?（1分）
由题图可知，小球在奇数秒内沿斜面做匀加速运动，在偶数秒内离开斜面做完整的圆周运动．?（1分）
所以，第五秒末的速度为：v5=a(t1+t3+t5)="6g" sinθ?⑥?（1分）
小球离开斜面的最大距离为：
d=2R3?⑦?（1分）
由以上各式得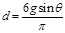：?（1分）
（3）第19秒末的速度：v19=a(t1+t3+t5+…+t19)="20g" sinθ?⑧?（1分）
小球未离开斜面的条件是：
qv19B≤（mg+qE0）cosθ?⑨（2分）
所以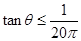：?（1分）

本题难度：一般