1、简答题  如图所示，粗细均匀的U形细玻璃管右端封闭，开口向下竖直放置，长L的横管中充满汞液，封住长L的右管中的气柱．不计温度变化，大气压强为P0．今将管晃动后又静止在竖直位置时，发现汞柱可能向右管移动些，也可能向左管移动些，也可能恢复原状．试指出与前二类情况对应的L的值．

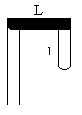
参考答案：
当L＞P0时，x＞0，汞柱向右管移；当L＜P0时，x＜0，汞柱向左管移

本题解析：
设晃动后汞柱向右管移动x后又静止．如图(2)，研究右管中被封住的气柱，因温度不变，所以有(P0+x)(L-x)S=P0LS (1)
（式中大气压的单位采用厘米汞柱）
-x2+(L-P0)x+LP0=P0L (2)
x2=(L-P0)x
x1=L-P0；x2=0（舍去）
可见，当L＞P0时，x＞0，汞柱向右管移；当L＜P0时，x＜0，汞柱向左管移．

本题难度：简单

2、计算题  如图所示是用导热性能良好的材料制成的气体实验装置，开始时封闭的空气柱长度为3 cm，此时气压表显示容器内压强p1＝1.0×105 Pa。求：
（1）将活塞缓慢向下推动，直到封闭空气柱长度变为2 cm时，气压表的示数是多少？
（2）将活塞快速向下推动，若在压缩气体过程中，气体内能增加了1.5 J，气体放出的热量为1.4 J，那么活塞对气体做的功是多少？

参考答案：解：（1）缓慢压缩时，气体温度不变，L0＝3 cm，L＝2 cm，p0＝1.0×105 Pa
设被压缩后气体压强为p，由玻意耳定律有：p0L0S＝pLS
解得：p＝1.5×105 Pa
（2）由热力学第一定律有：ΔU＝W＋Q
W＝ΔU－Q＝1.5－(－1.4)＝2.9 J

本题解析：

本题难度：一般

3、计算题  （7分）用传统的打气筒给自行车打气时，不好判断是否已经打足了气．某研究性学习小组的同学们经过思考，解决了这一问题．他们在传统打气筒基础上进行了如下的改装(示意图如图所示):圆柱形打气筒高H，内部横截面积为S，底部有一单向阀门K，厚度不计的活塞上提时外界大气可从活塞四周进入，活塞下压时可将打气筒内气体推入容器B中，B的容积VB＝3HS，向B中打气前A、B中气体初始压强均为p0，该组同学设想在打气筒内壁焊接一卡环C(体积不计)，C距气筒顶部高度为h＝H，这样就可以自动控制容器B中的最终压强．

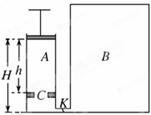
求：①?假设气体温度不变，则第一次将活塞从打气筒口压到C处时，容器B内的压强是多少？
② 要使容器B内压强不超过5p0，h与H之比应为多少？

参考答案：(1) pB＝1.2p0? (2)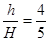

本题解析：①第一次将活塞从打气筒口压到C处时，设容器B内的压强为pB，C距低部H－h＝H/3，由玻意耳定律得p0(VB＋HS)＝pB(VB＋HS/3)?（2分）
解得? pB＝1.2p0?（1分）
②对打气筒内的气体，要使容器B内压强不超过5p0，意味着活塞从顶端下压至C处时，打气筒C处以下的压强不能超过5p0，由玻意耳定律得? p0HS=5p0(H－h)S?（2分）
解得?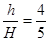?（2分）

本题难度：一般

4、计算题  如图，两端封闭、粗细均匀、竖直放置的玻璃管内，有一长为h的水银柱，将管内气体分为两部分，已知l2=2l1。若使两部分气体同时升高相同的温度，管内水银柱将如何运动？（设原来温度相同）

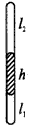
参考答案：解：水银柱原来处于平衡状态，所受合外力为零，即此时两部分气体的压强差△p=P1-P2=h。温度升高后，两部分气体的压强都增大，若△P1>△p2，水银柱所受合外力方向向上，应向上移动，若△P1<△P2，水银柱向下移动，若△p1=△P2，水银柱不动。所以判断水银柱怎样移动，就是分析其合力方向，即判断两部分气体的压强哪一个增大得多。
(1)假设法：
假设水银柱不动，两部分气体都做等容变化，分别对两部分气体应用查理定律：
上段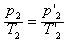：，所以，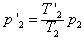
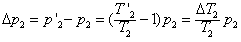
下段：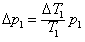
又因为△T2=△T1，T1=T2，P1=P2+h>P2
所以△P1>△P2，即水银柱上移
(2)图象法：
在同一p-T图上画出两段气柱的等容线，如图，因为在温度相同时，P1>P2，得气柱l1等容线的斜率较大，当两气柱升高相同的温度△T时，其压强的增量△P1>△P2，所以水银柱上移

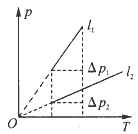
(3)极限法：
由于P2较小，设想P2=0，即上部为真空，升温 则p1增大，水银柱上移，降温下移

本题解析：

本题难度：一般

5、计算题  ）如图所示，在长为L=57cm的一端封闭、另一端开口向上的竖直玻璃管内，用4cm高的水银柱封闭着51cm长的理想气体，管内外气体的温度均为33℃ ，大气压强p0=76cmHg.

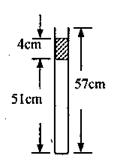
①若缓慢对玻璃管加热，当水银柱上表面与管口刚好相平时，求管中气体的温度；
②若保持管内温度始终为33℃，现将水银缓慢注入管中，直到水银柱上表面与管口相平，求此时管中气体的压强。

参考答案：①T2=318K②P2=85cmHg

本题解析：①设玻璃管横截面积为S，以管内封闭气体为研究对象， 气体经等压膨胀：
初状态：V1=51S，T1=306K
末状态：V2=53ST2=？ （1分）
由盖—吕萨克定律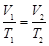：（2分）得T2=318K   （1分）
②当水银柱上表面与管口相平，设此时管中气体压强为P，水银柱的高度为H，管内气体经等温压缩：
初状态：V1=51S    P1= 80cmHg  （1分）
末状态：V2?=(57-H)S    P2="(76+H)" cmHg （1分）
由玻意耳定律：P1 V1 =P2V2?（2分）
得 H=9cm（1分）
故P2=85cmHg（1分）
考点：考查了理想气体状态方程的应用

本题难度：一般