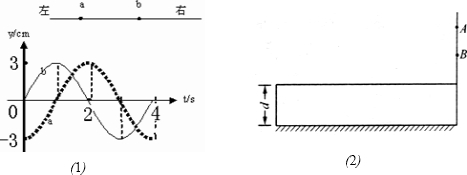
1、简答题  （1）一列简谐横波沿直线ab向右传播，a、b两点之间沿波的传播方向的距离为2m，a、b两点的振动情况如图（1）所示，下列说法中正确的是______

A．波速可能大于

参考答案：

（1）由振动图象可知，在t=0时刻，a位于波谷，b经过平衡位置向上，结合波形可知，a、b两点间的距离△x=（n+34）λ，（n=0，1，2…）
得? λ=4△x4n+3，则波速为v=λT=△x4n+3=24n+3m/s
可见，v的最大值为23m/s．
当n=1时，v=27m/s．
故选B
（2）作出光路图，光束入射角i=90°-30°=60°
由n=sinisinr得：r=30°
由几何关系有：CEsin30°=ABsin60°
且CE=2dtsnr
代入数据解得：d=6cm
故答案为：
（1）B
（2）此玻璃砖的厚度d=6cm．

本题解析：

本题难度：一般

2、计算题  渔船常利用超声波来探测远处鱼群的方位．已知某超声波频率为1.0×105 Hz，某时刻该超声波在水中传播的波动图像如图所示．

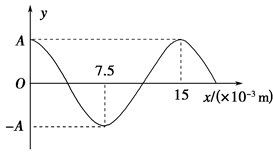
(1)从该时刻开始计时，画出x＝7.5×10－3 m处质点做简谐运动的振动图像(至少一个周期)．
(2)现测得超声波信号从渔船到鱼群往返一次所用时间为4 s，求鱼群与渔船间的距离(忽略船和鱼群的运动)．

参考答案：(1)如下图　(2)3 000 m

本题解析：(1)该波的周期为T＝＝1×10－5 s，由波动图像知，此时x＝7.5×10－3 m处的质点位于负的最大位移处，所以，从该时刻开始计时，该质点的振动图像如图所示．

(2)由波形图读出波长λ＝15×10－3 m
由波速公式得
v＝λf?①
鱼群与渔船的距离为x＝vt?②
联立①②式，代入数据得x＝3 000 m?③

本题难度：一般

3、填空题  一列简谐横波沿x轴正方向传播，t=0时刻的图像如图所示，周期T＝0.01s，介质中质点P位于x＝2 m处。则该列波传播的速度大小为?m/s。t＝0.15 s时质点P振动方向_______（填写“+y”或“-y”）。

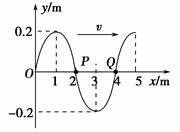
参考答案：400　 +y

本题解析：由图知，波长为4m，所以波速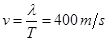；0.15s时质点P处于下坡阶段，根据上下坡法知P点向上振动即+y方向

本题难度：简单

4、选择题  如图所示，在平面xOy内有一沿x轴正方向传播的简谐横波，波速为3.0m/s，频率为2.5Hz，A、B两点位于x轴上，相距0.90m．分别以A、B为平衡位置的两个质元在振动过程中，取A点的质元位于波峰时为t=0，对于B点的质元来说（　　）
A．t=0时，加速度最大
B．t=0.1s时，速度为零
C．t=0.2s时，速度方向沿y轴负方向
D．t=0.3s时，位于波谷